Dynamic analysis and control of a rice-pest system under transcritical bifurcations

Study area

This study has been conducted globally without being confined to a specific region because food security and pest management are global issues. It is not possible to reduce the annual loss of rice and control pest infestation by adopting certain control strategies in certain areas of a country. Here, we consider two control strategies, cultural methods and chemical control, to increase the annual production of rice by controlling the pests in the paddy field. Cultural methods which consist of natural controls such as soil rotation, crop variation, and natural enemies are used as the first and foremost control strategy because of having natural capacity of increasing the production of rice and controlling rice pests. On the other hand, chemical controls consisting of various pesticides such as neonicotinoids, glyphosate, DDT, BHC, and 2,4-D are used only for emergency situations because of having adverse effects on the environment and crop quality. Here, we do not define any specific pesticide because pesticides can vary from pest to pest. Besides, the cultivation areas/lands are decreasing due to deforestation and urbanization, so the total cultivation areas are not constant and change every year. To avoid the effect of this contradiction in this study, the annual production of rice is considered and calculated in metric tons per hectare area (Mt/h).

Lotka–Volterra model in an optimal control problem setting

The general form of the Lotka–Volterra model can be written in terms of a pair of autonomous differential equations (1)${\displaystyle \left\{\begin{array}{c}\dot{x}=xf\left(x,y\right)\hfill \\ \dot{y}=yg\left(x,y\right)\hfill \end{array}\right.}$

with x and y being the prey and predator populations and f(x, y) and g(x, y) being the species’ growth rates.

The optimal control problem (OCP) of the Lotka–Volterra model is to find control variable sets to optimize (minimize or maximize) a specific objective function (Lenhart & Workman, 2007), subject to constraints on the state variables. To define how an OCP is concerned with the state and the control variables, consider x(t) and u(t) are these two variables of an OCP respectively, x(t) satisfies (2)${\displaystyle \dot{x}\left(t\right)=g\left(t,x\left(t\right),u\left(t\right)\right)}$

with g being continuously differentiable. An OCP can be described in the following way. (3)${\displaystyle \begin{array}{c}\text{Maximize or minimize}J\left(x,u\right)={\int }_a^{b}L\left(t,x\left(t\right),u\left(t\right)\right)dt\hfill \\ \text{Subject to}\dot{x}\left(t\right)=g\left(t,x\left(t\right),u\left(t\right)\right)a.e.t\in \left[a,b\right]\hfill \\ u\left(t\right)\in U,\forall t\in \left[a,b\right]\hfill \\ x\left(a\right)\in x_0\mathrm{and}x\left(b\right)\in {\mathbb{R}}^{+}\mathrm{is free}\hfill \end{array}}$

with u(t) and x(t) both being piecewise C¹ differentiable with t in [a, b] being the time interval where a, b ∈ ℝ⁺ and a < b. In the problem, u(t) belongs to a certain space U that may be a piecewise continuous function or a space of measurable function which satisfies all the constraints of the problem. Therefore, (x^∗, u^∗) constitutes the optimal solution of the OCP in case the costs can be minimized overall admissible processes (Lenhart & Workman, 2007).

Dynamical modelling in form of a hybrid natural/chemical IPM strategy

Portions of this text were previously published as part of a preprint (Mandal et al., 2022).

Assumption and formulation of the optimal control problem

Wiping out the entire pest population from the agricultural field is impossible, and an attempt can be unsafe, expensive, and may lead to a rebound in pest numbers (IPM, 2021). To control the pest population, we first apply cultural methods that are safe, cheap, and easily applicable. We then model the application of chemical controls (pesticides) only when the unacceptable action thresholds are crossed (IPM, 2021). The application of pesticides depends on the species of pest and their density.

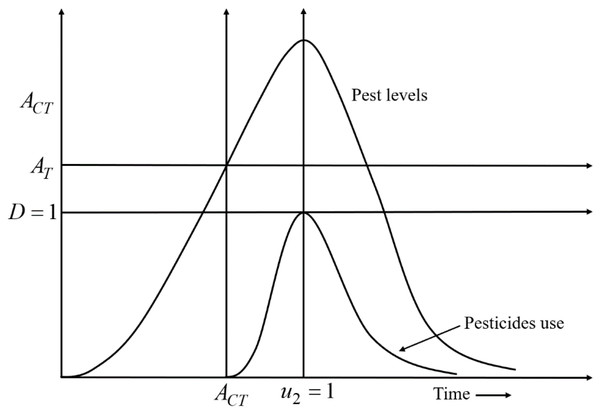
An important question is the determination of the point in time when to apply pesticides and for how long it should continue. Let u₁ denote cultural methods which are used incessantly throughout the entire cultivation period because they are natural and safe. Let u₂ denote chemical controls (pesticides) which are used only when the pest level crosses the acceptable threshold. The controls u₁ and u₂ both take values between 0 and 1. Here, u₁, u₂ = 0 denote that no control is applied and u₁, u₂ = 1 indicate controls are applied with full effort. Let A_T denote the unacceptable threshold (or action threshold) to determine the application of pesticides to control the pest population, and A_CT represents the interval in which pesticides should be applied. The unacceptable threshold can be defined as: A_T = μΔ, where µdenotes an unacceptable pest population per unit area and Δ represents the total area of a field. The threshold can depend on the pest variety, pest size, and site/region (IPM, 2021). For an increase in crop damaging pests, pesticides for their control are applied which may cause additional environmental impact through spreading via wind or rainwater into nearby ecosystems. Let D(x₂, u₂, E) denote the damage function of the nearby ecosystems which is potentially subject to excessive pesticide application, with x₂ being the pest population and E representing the environmental pollution. E is defined in the interval [0, 1] with E = 1 denoting that the pollution reaches the maximally acceptable level (E = 0 denotes zero pollution). The damage function, D, is increased in the rise of E, but the application of u₂ is decreased in the increase of D, where D ∈ [0, 1] (Lichtenberg & Zilberman, 1986; Waterfield & Zilberman, 2012). D = 1 represents the maximally acceptable damage threshold, meaning the application of pesticides should be stopped i.e., u₂ = 0. Conversely, D = 0 denotes that there is no damage, meaning pesticides can be applied with full effort i.e., u₂ = 1. Here E is proportionally increased with the application of u₂. If the pest species population crosses the action threshold, pesticides are employed i.e., $u_2\left(t\right)\in \left(\right.0,1\left.\right]\text{when}{x}_2\left(t\right)>A_T$ which increases the environmental pollution i.e., E ∈ (0, 1]. If E → 1 as u₂ → 1 which leads D → 1 that means the use of pesticides should be stopped immediately i.e., u₂ = 0. To reflect this, the following decision model has been developed: (4)${\displaystyle F\left(D,t\right)=\left\{\begin{array}{c}\left.\begin{array}{c}{u}_1\left(t\right)\in \left[0,1\right]\hfill \\ u_2\left(t\right)=0\hfill \end{array}\right\},\forall x_2\left(t\right)\le A_T\hfill \\ \left.\begin{array}{c}{u}_1\left(t\right),u_2\left(t\right)\in \left[0,1\right]\hfill \\ u_2\left(t\right)=1-D\left(x_2\left(t\right),u_2\left(t\right),E\left(t\right)\right)\hfill \end{array}\right\},\forall x_2\left(t\right)>A_T\hfill \end{array}\right.}$

where D is defined as, $D\left(x_2,u_2,E\right)=\left\{\begin{array}{c}D=0when{u}_2,E=0,\forall x_2\left(t\right)\le A_T\hfill \\ \left.\begin{array}{c}0<D<1when{u}_2,E\in \left(0,1\right)\hfill \\ D=1when{u}_2,E=1\hfill \end{array}\right\},\forall x_2\left(t\right)>A_T\hfill \end{array}\right.$.

A decision-making diagram of the model is expressed by Eq. (4) which describes the best time for the applications of pesticides is presented in Fig. 2. According to Fig. 2, when x₂ crosses the A_T line, u₂ is applied. Due to the applications of u₂, the growth rate of x₂ gradually slows down. When u₂ is applied at full scale (u ₂ =1), the growth rate of x₂ starts decreasing after reaching a stable situation. Because u ₂ =1, D reaches the maximum level i.e., D =1; the use of pesticides is stopped (u ₂ =0) to mitigate the adverse effect of pesticides on the environment and nearby ecosystems.

A control model is formulated on a developed rice-pest model, expressed by Eq. (S4) presented in Supplemental Information 1, where cultural methods and chemical controls are applied as two control variables aiming to minimize the density of rice pests. The dynamic relationships between the annual production of rice and the pest population under control are described below:

1. When cultural methods are applied during cultivation, the production rate of rice increases rapidly. Since cultural methods can directly increase the production of rice and the use of cultural methods does not depend on the density of rice pests, let u₁x₁ be the increment in the production of rice due to cultural methods. The first equation of the rice-pest system (S4) can be represented by including control as (5)${\displaystyle \frac{d}{dt}{x}_1\left(t\right)=\left({\alpha }_1-{\beta }_1{x}_2\left(t\right)\right)x_1\left(t\right)-d_1{x}_1^2\left(t\right)+u_1\left(t\right)x_1\left(t\right)}$ here, x₁(t) represents the annual production of rice per unit area (Mt/h), α₁ shows the reproduction rate of rice, β₁ represents the loss rate of x₁(t) due to the consumption of pests, d₁ presents the decrease rate due to intraspecific competition in species x₁(t) due to natural causes that are not related to pests e.g., viral infections, droughts or floods (Bazykin, 1976; Liu & Jiang, 2021). Please note that pesticides do not directly increase the production of rice, but directly control the level of pest species causing an indirect increase of rice production. Since the term “ β₁x₂x₁” in Eq. (5) represents the impact of pest density, no additional term is required to present the effect of pesticides on the rice production.

2. When cultural methods are applied in rice cultivation, several rice pests die off because of soil rotation and the presence of predators. Therefore, the cultural methods decline the density of rice pests and let u₁x₁x₂ be the declining number of pests due to the adoption of cultural methods. On the other hand, when emergency situations, pesticides are applied according to Eq. (4), which significantly reduces the pest population. Since the application of pesticides depends on the density of insect pests, let u₂x₁x₂ be the decline in the density of pest population after the use of pesticides. Hence, the second equation of the rice-pest system (S4) can be represented considering the decision model Eq. (4) as in the following: (6)${\displaystyle \frac{d}{dt}{x}_2\left(t\right)=\left({\beta }_2{x}_1\left(t\right)-{\alpha }_2\right)x_2\left(t\right)-d_2{x}_2^2\left(t\right)-F\left(D,t\right)x_1\left(t\right)x_2\left(t\right)}$ here, x₂(t) represents the density of rice pests at time t, β₂ shows the energy gain rate of pest population by consuming rice, α₂ represents the decline rate of the pest’s population proportionally with the decline of rice production, d₂ shows the decrease rate due to intraspecific competition between x₂(t) due to natural causes that not related to x₁(t), e.g., viral infection and heavy rains (Bazykin, 1976; Yang, 2020). Here, the term F(D, t)x₁x₂ corresponds to u₁x₁x₂ and u₂x₁x₂ since the decision model Eq. (4), defined by F(D,t), decides the application of the control variables u ₁ and u ₂.

The modified rice-pest system (S4) under controls and decision model Eq. (4) can be represented by arranging Eqs. (5) and (6) as in the following: (7)${\displaystyle \left\{\begin{array}{c}\frac{d}{dt}{x}_1\left(t\right)=\left({\alpha }_1-{\beta }_1{x}_2\left(t\right)\right)x_1\left(t\right)-d_1{x}_1^2\left(t\right)+u_1\left(t\right)x_1\left(t\right)\hfill \\ \frac{d}{dt}{x}_2\left(t\right)=\left({\beta }_2{x}_1\left(t\right)-{\alpha }_2\right)x_2\left(t\right)-d_2{x}_2^2\left(t\right)-F\left(D,t\right)x_1\left(t\right)x_2\left(t\right)\hfill \\ x\left(t\right)=\left(x_1\left(t\right),x_2\left(t\right)\right),\forall t\hfill \\ x\left(t\right)=\left(x_{10},x_{20}\right),whent=0\hfill \end{array}\right.}$

Therefore, the system defined by Eq. (7) represents the rice-pest-control model, in Lotka–Volterra form complemented by a decision model Eq. (4). The decision model (Eq. (4)) controls the results of the rice-pest-control model Eq. (7) and mitigates the adversity of pesticides by controlling their use.

For more details, please look at Supplemental Information 1 for rice-pest system (S4) formulation and analysis, and Supplemental Information 2 for transcritical bifurcation analysis for the rice-pest system (S4).

The characteristics of the controls are represented in the following measurable control set. (8)${\displaystyle U=\left\{\left(u_1\left(t\right),u_2\left(t\right)\right):0\le u_i\left(t\right)\le 1,i=1,2\mathrm{at}t\in \left[0,T\right]\right\}}$

where T is a preselected period for applied controls. The objective function of the control model Eq. (7) becomes (9)${\displaystyle \text{Minimize}J\left(x,u\right)={\int }_0^T\left(x_2\left(t\right)+\frac{A}{2}{u}_1^2+\frac{B}{2}{u}_2^2\right)dt}$

The optimal control model which approximates model Eq. (7) can be represented (Lenhart & Workman, 2007) as: (10)${\displaystyle \left\{\begin{array}{c}\text{Minimize}J\left(x,u\right)={\int }_0^T\left(x_2\left(t\right)+\frac{A}{2}{u}_1^2+\frac{B}{2}{u}_2^2\right)dt\hfill \\ \text{Subject to}{x}^{\prime }=g\left(t,x\left(t\right),u\left(t\right)\right)\hfill \\ u\left(t\right)\in U,\forall t\in \left[0,T\right]\hfill \\ x\left(0\right)=x_0\hfill \end{array}\right.}$

where $x\left(t\right)=\left(\begin{array}{c}{x}_1\left(t\right)\hfill \\ x_2\left(t\right)\hfill \end{array}\right)$, $g\left(t,x\left(t\right),u\left(t\right)\right)=\left(\begin{array}{c}\left({\alpha }_1-{\beta }_1{x}_2\left(t\right)\right)x_1\left(t\right)-d_1{x}_1^2\left(t\right)+u_1\left(t\right)x_1\left(t\right)\hfill \\ \left({\beta }_2{x}_1\left(t\right)-{\alpha }_2\right)x_2\left(t\right)-d_2{x}_2^2\left(t\right)-F\left(D,t\right)x_1\left(t\right)x_2\left(t\right)\hfill \end{array}\right)$ and $u\left(t\right)=\left(\begin{array}{c}{u}_1\left(t\right)\hfill \\ u_2\left(t\right)\hfill \end{array}\right)$; 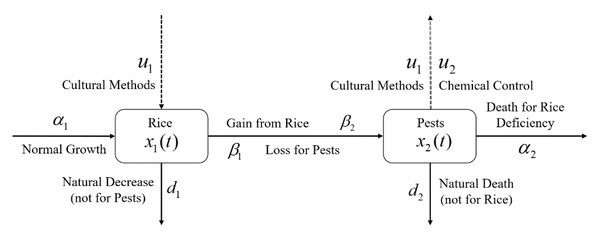A and B are used for cost balancing weight parameters for the control variables u₁ and u₂, respectively; the function g is continuously differentiable; and functions u(t) and x(t) are piecewise continuous differentiable. In this problem, u(t) belongs to a certain space U that may be a piecewise continuous function or a space of measurable functions which satisfy all constraints of the problem. The main goal of the objective function is to increase the annual rice yield by minimizing the pest population by simultaneously considering the controls with the lowest costs. A schematic diagram of the rice-pest-control system Eq. (7) is shown in Fig. 3 to illustrate the dynamic behaviour of the species under control.

Characterization of the optimal control

To estimate the necessary conditions for the optimality of the optimal control problem Eq. (10), Pontryagin’s maximum principle has been imposed in terms of the Hamiltonian H(t) defined as Lenhart & Workman (2007) ${\displaystyle H\left(t,x,u,\lambda \right)=L\left(t,x,u\right)+\sum _{i=1}^2{\lambda }_{i}g\left(t,x,u\right)=x_2\left(t\right)+\frac{A}{2}{u}_1^2\left(t\right)+\frac{B}{2}{u}_2^2\left(t\right)+{\lambda }_1\left[\left({\alpha }_1-{\beta }_1{x}_2\left(t\right)\right)x_1\left(t\right)-d_1{x}_1^2\left(t\right)+u_1\left(t\right)x_1\left(t\right)\right]+{\lambda }_2\left[\left({\beta }_2{x}_1\left(t\right)-{\alpha }_2\right)x_2\left(t\right)-d_2{x}_2^2\left(t\right)-F\left(D,t\right)x_1\left(t\right)x_2\left(t\right)\right]}$

where λ_i, i = 1, 2 is the co-state variable which satisfies the following adjoint equations,

$\frac{d{\lambda }_1}{dt}=-\frac{dH\left(t,x,u,\lambda \right)}{d{x}_1\left(t\right)}$ $=-{\lambda }_1\left[\left({\alpha }_1-{\beta }_1{x}_2\left(t\right)\right)-2d_1{x}_1\left(t\right)+u_1\left(t\right)\right]-{\lambda }_2\left[{\beta }_2{x}_2\left(t\right)-F\left(D,t\right)x_2\left(t\right)\right]$, and

$\frac{d{\lambda }_2}{dt}=-\frac{dH\left(t,x,u,\lambda \right)}{d{x}_2\left(t\right)}$ $=-1+{\lambda }_1{\beta }_1{x}_1\left(t\right)+{\lambda }_2\left[\left({\alpha }_2-{\beta }_2{x}_1\left(t\right)\right)+2d_2{x}_2\left(t\right)+F\left(D,t\right)x_1\left(t\right)\right]$

as well as the transversality conditions λ₁(T) = 0 and λ₂(T) = 0.

Now, to obtain the optimal solution of the controls, Theorem 3.1, and Theorem 3.2 must be proven as shown below by applying Pontryagin’s maximum principle.

Theorem 3.1. The control variables for the acceptable damage threshold attain the optimal solutions

$\left({u_1}_{\ast },{u_2}_{\ast }\right)=\left(max\left\{0,min\left(1,\frac{{\lambda }_2{x_1}_{\ast }{x_2}_{\ast }-{\lambda }_1{x_1}_{\ast }}{A}\right)\right\},0\right)$ for which the objective function J over U is minimized.

Proof At the acceptable damage threshold, there is no use of pesticides i.e., u₂ = 0. Therefore, let’s differentiate the Hamiltonian (H) with respect to the control variable u₁ only, then it becomes as (11)${\displaystyle \frac{dH}{d{u}_1}=A{u}_1+{\lambda }_1{x}_1-{\lambda }_2{x}_1{x}_2}$

By applying the conditions of optimality in Eq. (11), the characterization of the control variable u₁

1. when $\frac{dH}{d{u}_1}>0$ then $u_1>\frac{{\lambda }_2{x}_1{x}_2-{\lambda }_1{x}_1}{A}$ but for the minimization problem u₁ = 0

2. when $\frac{dH}{d{u}_1}=0$ then $u_1=\frac{{\lambda }_2{x}_1{x}_2-{\lambda }_1{x}_1}{A}$

3. when $\frac{dH}{d{u}_1}<0$ then $u_1<\frac{{\lambda }_2{x}_1{x}_2-{\lambda }_1{x}_1}{A}$ but for the minimization problem u₁ = 1

Therefore $u_1^{\ast }=\left\{\begin{array}{c}1whendH/d{u}_1<0\hfill \\ \frac{{\lambda }_2{x}_1{x}_2-{\lambda }_1{x}_1}{A}whendH/d{u}_1=0\hfill \\ 0whendH/d{u}_1>0\hfill \end{array}\right.$, which can be written in the following compact form

${u_1}_{\ast }=max\left\{0,min\left(1,\frac{{\lambda }_2{x_1}_{\ast }{x_2}_{\ast }-{\lambda }_1{x_1}_{\ast }}{A}\right)\right\}$.

Since u₂ = 0 at the acceptable threshold, the compact form of u₂ is u_2∗ = 0. Then, the optimal solutions of the control variables for the acceptable threshold are

$\left({u_1}_{\ast },{u_2}_{\ast }\right)=\left(max\left\{0,min\left(1,\frac{{\lambda }_2{x_1}_{\ast }{x_2}_{\ast }-{\lambda }_1{x_1}_{\ast }}{A}\right)\right\},0\right)$,

hence, it completes the proof.

Theorem 3.2. The control variables for the action threshold attain the optimal solutions

$\left(u_1^{\ast },u_2^{\ast }\right)=\left(max\left\{0,min\left(1,\frac{{\lambda }_2{x}_1^{\ast }{x}_2^{\ast }-{\lambda }_1{x}_1^{\ast }}{A}\right)\right\},max\left\{0,min\left(1,\frac{{\lambda }_2{x}_1^{\ast }{x}_2^{\ast }}{B}\right)\right\}\right)$ for which the objective function J over U is minimized.

Proof: For the action threshold, the decision model is fully active i.e., F(D, t) = u₁(t) + u₂(t). Therefore, let’s differentiate the Hamiltonian (H) with respect to the control variables u₁ and u₂, then it becomes as

(12)${\displaystyle \frac{dH}{d{u}_1}=A{u}_1+{\lambda }_1{x}_1-{\lambda }_2{x}_1{x}_2}$ (13)${\displaystyle \frac{dH}{d{u}_2}=B{u}_2-{\lambda }_2{x}_1{x}_2}$

By applying the conditions of optimality in Eq. (12), the characterization of the control variable u₁

1. when $\frac{dH}{d{u}_1}>0$ then $u_1>\frac{{\lambda }_2{x}_1{x}_2-{\lambda }_1{x}_1}{A}$ but for the minimization problem u₁ = 0

2. when $\frac{dH}{d{u}_1}=0$ then $u_1=\frac{{\lambda }_2{x}_1{x}_2-{\lambda }_1{x}_1}{A}$

3. when $\frac{dH}{d{u}_1}<0$ then $u_1<\frac{{\lambda }_2{x}_1{x}_2-{\lambda }_1{x}_1}{A}$ but for the minimization problem u₁ = 1

Therefore $u_1^{\ast }=\left\{\begin{array}{c}0whendH/d{u}_1>0\hfill \\ \frac{{\lambda }_2{x}_1{x}_2-{\lambda }_1{x}_1}{A}whendH/d{u}_1=0\hfill \\ 1whendH/d{u}_1<0\hfill \end{array}\right.$, which can be written in the following compact form

$u_1^{\ast }=max\left\{0,min\left(1,\frac{{\lambda }_2{x}_1^{\ast }{x}_2^{\ast }-{\lambda }_1{x}_1^{\ast }}{A}\right)\right\}$.

Similarly, by applying the conditions of optimality in Eq. (13), the characterization of the control variable u₂ becomes

$u_2^{\ast }=\left\{\begin{array}{c}0whendH/d{u}_2>0\hfill \\ \frac{{\lambda }_2{x}_1{x}_2}{B}whendH/d{u}_2=0\hfill \\ 1whendH/d{u}_2<0\hfill \end{array}\right.$, which can be written in the following compact form

$u_2^{\ast }=max\left\{0,min\left(1,\frac{{\lambda }_2{x}_1^{\ast }{x}_2^{\ast }}{B}\right)\right\}$.

Then, the optimal solutions of the control variables are

$\left(u_1^{\ast },u_2^{\ast }\right)=\left(max\left\{0,min\left(1,\frac{{\lambda }_2{x}_1^{\ast }{x}_2^{\ast }-{\lambda }_1{x}_1^{\ast }}{A}\right)\right\},max\left\{0,min\left(1,\frac{{\lambda }_2{x}_1^{\ast }{x}_2^{\ast }}{B}\right)\right\}\right)$.

Hence the theorem completes the proof.

Numerical investigations of the rice-pest system (S4)

Both the time series and phase portrait of the considered dynamics are shown in Fig. 4. Initially, the growth of the rice plants sharply increases due to low numbers in the pest population. When the pest population increases by getting sufficient food, the growth of the rice plants is hampered so that eventually the pest population subdues (which in turn allows rice to grow again) (Vargas & Nishida, 1980; IPM, 2021). The phase portrait is shown in Fig. 4B spiralling out to a stable equilibrium at $\left({\hat{x}}_1\left(t\right),{\hat{x}}_2\left(t\right)\right)=\left(4.12,11.54\right)$ (Dym, 2004; Youssef & Raffoul, 2022).

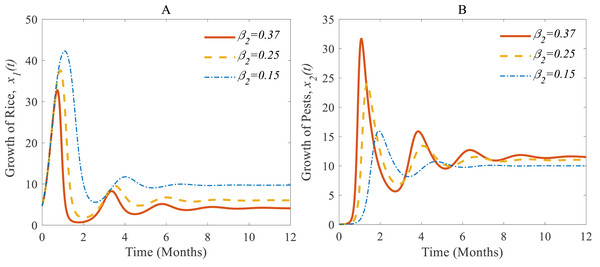
Figures 5A and 5B show (i) when the consumption rate β₂ of the pest population is reduced from 37% to 25%, the density of pest population decreases so that the rice is increasing again (Vargas & Nishida, 1980; IPM, 2021). Similarly, in (ii): when the consumption rate declines from 25% to 15%, the density of pests declines sharper than before, and the rice grows better again (Oerke et al., 1994; IPM, 2021).

According to the result of Fig. 4A, the annual production of rice approaches 4.12 Metric tons/hector (Mt/h) whereas the growth rate of pests approaches 11.54%. The changes in the growth of rice for different consumption rates of pests are described in Fig. 5 which let us conclude that the production of rice can be increased if the consumption rate of pests is controlled.

Numerical investigations of the rice-pest-control system (Eq. (7))

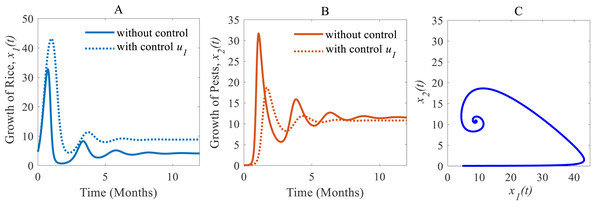
When controls are applied to the rice-pest model (S4), the results change. The results of the rice-pest-control system Eq. (7) are described for the following three scenarios designed on the efficacy of the control variable u₁ (cultural methods) and u₂ (chemical controls): (i) u₁ = 0.2 ∈ (0, 1] and u₂ = 0, (ii) u₁ = 0 and u₂ = 0.26 ∈ (0, 1], and (iii) u₁ = 0.1 ∈ (0, 1] and u₂ = 0.2 ∈ [0, 1]. The simulations are performed distinguishing the cases “without control” and “with control”. Here, “without control” represents the results of the rice-pest system (S4) meaning there is no control strategy (u₁ = 0, u₂ = 0). The applications of controls are restricted by decision model Eq. (4) whereas pesticides are only applied in emergency situations to reduce the adverse effects of pesticides. Since the applications of pesticides are decided on the pest density, cultivation conditions and environmental factors, the decisions for the application of pesticides can vary over time and situations. Therefore, the application of u ₂ can be applied just only once or several times, or maybe totally avoided.

(i) When only the cultural methods are implemented to the system as a control variable, the annual losses of rice decline from 41.05 to 38.39 MMT approximately, at the same time, the production rate of rice increases from 4.12 to 8.81 Mt/h approximately (Peshin & Dhawan, 2009; IPM, 2021; Milligan et al., 2016) which are shown in Fig. 6A. As a result of adopting cultural methods, the density of rice pests declines from 11.54% to 10.79% approximately over one period due to e.g., the enhancement of soil and rotation of crops (Peshin & Dhawan, 2009; IPM, 2021; Milligan et al., 2016) as shown in Fig. 6B. Figure 6C shows that the system under the application of cultural methods converges to the stable equilibrium point at $\left({\hat{x}}_1\left(t\right),{\hat{x}}_2\left(t\right)\right)=\left(8.81,10.79\right)$.

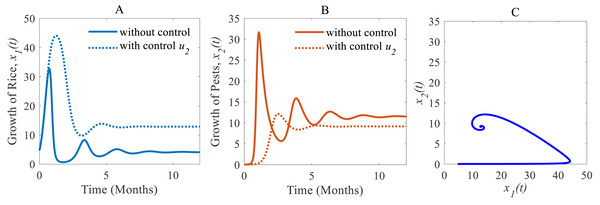
(ii) When only the chemical control is implemented according to the condition expressed in Eq. (4), the pest population comes down from 11.54% to 9.17% approximately that’s just over one-fifth of the total population (Inao et al., 2008; Bhattacharyya & Bhattacharya, 2006) as shown in Fig. 7B. Because of the decreasing pest population, the annual losses of rice drop sharply from 41.05 to 32.62 MMT approximately with a decrease approximating 25%. As a result, the annual rice production rate substantially grows from 4.12 to 12.86 Mt/h approximately (Inao et al., 2008; Marinelli, 2005) which is shown in Fig. 7A. The system converges to a stable equilibrium point at $\left({\hat{x}}_1\left(t\right),{\hat{x}}_2\left(t\right)\right)=\left(12.86,9.17\right)$, presented in Fig. 7C.

(iii) When the cultural methods are used continuously, chemical controls are according to decision model Eq. (4) only applied in an emergency i.e., only when the pest population density crosses the action threshold, which leads in a consequence to a decrease of the pest population, e.g., as shown in Fig. 8B from 33.02% to 7.73% (Inao et al., 2008; Peshin & Dhawan, 2009; IPM, 2021; Milligan et al., 2016). As a result, the annual losses of rice dramatically fall from about 41.05 to 27.49 MMT. After simultaneously applying controls the annual rice production increases considerably and reaches 19.18 Mt/h (Inao et al., 2008; Peshin & Dhawan, 2009; Milligan et al., 2016) as presented in Fig. 8A thereby approaching the equilibrium point $\left({\hat{x}}_1\left(t\right),{\hat{x}}_2\left(t\right)\right)=\left(19.18,7.73\right)$ as shown in Fig. 8C. The phase plane (Fig. 8C) reveals that the system with two controls stabilizes faster than the system with only one control.

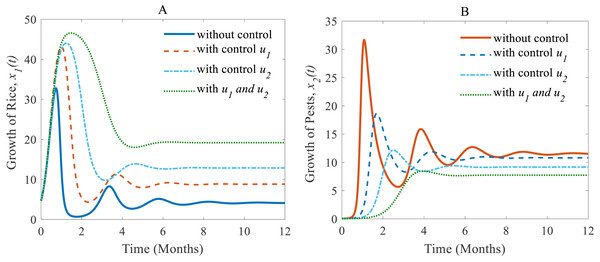
Next, we made a numerical comparison to analyse the results of all situations. The dynamic changes in the growth of the state variables in the three scenarios are shown in Fig. 9. As can be seen from Fig. 9, the annual production of rice increases significantly under both control strategies instead of just one, in contrast, the rice pests decrease dramatically. It also shows that cultural methods can control the density of the pest population, but chemical controls are comparatively more effective. From scenarios (i) to (iii), it is concluded that scenario (iii) is the best strategy to increase the annual rice production and reduce the density of rice pests.

Significance of β as a transcritical bifurcation parameter

Furthermore, the rice-pest model (S4) is experienced a transcritical bifurcation analysis and the dimensionless rice-pest model (S16) has been numerically investigated for the variation in the growth of pest populations (β) by employing MATLAB, where the dimensionless parameters α = 1 and γ = 0.001 (for more details, see Supplemental Information 2).

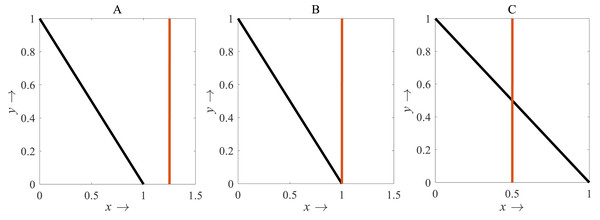
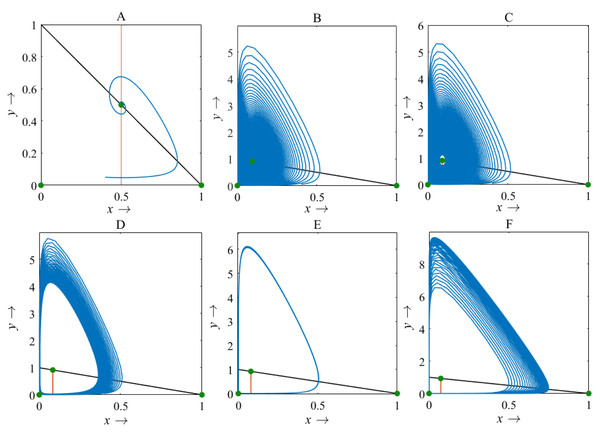
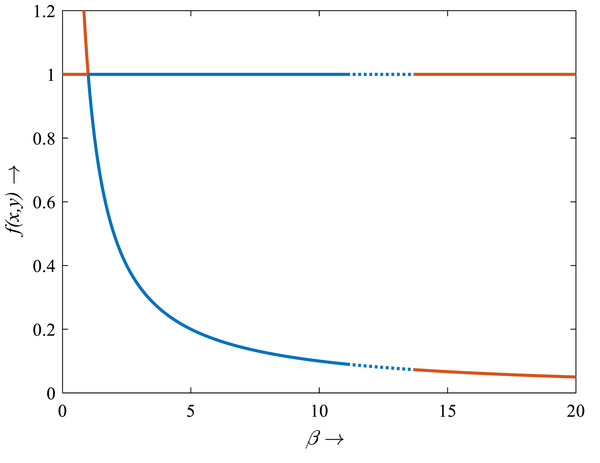
For β < 1, there is no intersection between the rice isocline and pests isocline as represented in Fig. 10A. In this case, the system (S16) experiences unstable and no equilibrium point (Banerjee & Petrovskii, 2011). For β = 1, the isoclines of rice and pests intersect at the pest-free equilibrium point E₁(1, 0) as shown in Fig. 10B. For β > 1, the system (S16) experiences an interior point E_∗(x_∗, y_∗) between the origin (0, 0) and E₁(1, 0) as represented in Fig. 10C (Perko, 2000; Sen, Banerjee & Morozov, 2012). The nature of the system (S16) is illustrated at the interior equilibrium point E_∗(x_∗, y_∗) for the different values of β > 1 which is described in Fig. 11. The rice-pest system (S16) is stable at the interior critical point E_∗ for the bifurcation parameter β ∈ (1, 11]; e.g., the system is stable for choices of β = 2 and β = 10.9 as shown in Figs. 11A and 11B, respectively. For β = 11.1, there is a stable limit cycle at E_∗ as shown in Fig. 11C. The system experiences a limit cycle for the parameter β ∈ [11.1, 13.6] which remains at a steady state, as presented in Figs. 11D to 11F. The steady state becomes unsteady state for β = 13.7 and thus the sytem becomes unstable for all β > 13.6 (for more details, see Fig. S3). Hence, the maximum value of β is β^∗ = 13.6. Moreover, the transcritical bifurcation diagram with respect to the bifurcation parameter β has been carried out, as represented in Fig. 12. The diagram also describes that the dimensionless rice-pest system (S16) is stable for β ∈ (1, 11] and experienes steady state limit cycle for β ∈ [11.1, 13.6] and gradually tends to an imbalance situation with the increase of the growth of the pest populations (β) and even the system will be defeated for high growth rate (β > 13.6). Hence the bifurcation analysis suggests to control the pest population for the sustainable management of the rice-pest system (S4), otherwise, the high pest populations will likely reduce the ‘rice’ response to zero.