An improved hybrid whale optimization algorithm for global optimization and engineering design problems

Encircling prey

During the encircling prey stage, the WOA algorithm emulates the ability of humpback whales to recognize the prey’s position and encircle them. In each iteration, the best solution, acting as the leader, is considered the target prey. The behavior is defined in Eqs. (1)–(3): (1)${\displaystyle \overrightarrow{X}\left(t+1\right)={\overrightarrow{X}}_{Leader}\left(t\right)-\overrightarrow{A}\odot \overrightarrow{D}}$ (2)${\displaystyle \overrightarrow{A}=2a.\overrightarrow{r}-a}$ (3)${\displaystyle \overrightarrow{C}=2.\overrightarrow{r}}$

where, t represents the iteration number, $\overrightarrow{A}$ and $\overrightarrow{C}$ are the coefficient vectors of WOA, ${\overrightarrow{X}}_{Leader}$ denotes the position vector of the best solution found so far, and $\overrightarrow{X}$ represents the position vector of each member in the algorithm population. Furthermore, the ⊙ sign denotes the element-wise multiplication. Notably, to enhance the performance of WOA, the value of a linearly declines from 2 to zero during the iterations, and $\overrightarrow{r}$ is a vector of uniformly distributed random numbers between zero and one.

Exploitation stage: bubble-net attacking maneuver

The bubble-net attacking maneuver, inspired by the hunting behavior of humpback whales, is modeled using two strategies:

1. Declining surrounding strategy: This strategy is achieved by reducing the value of a in Eq. (2). Notably, the range of variation in vector $\overrightarrow{A}$ is directly proportional to a, where $\overrightarrow{A}$ consists of randomly generated values between - a and a.

2. Spiral position update: The whale’s displacement towards the prey’s position, simulating the spiral motion of humpback whales, is formulated as Eq. (4): (4)${\displaystyle \overrightarrow{X}\left(t+1\right)={\overrightarrow{X}}_{Leader}\left(t\right)+\overrightarrow{D^{\prime }}.e^{B.L}.Cos\left(2\pi L\right)}$

where $\overrightarrow{D^{\prime }}=\left|{\overrightarrow{X}}_{Leader}-\overrightarrow{X}\right|$ denotes how far is the ith whale from the prey, B is a constant that describes the logarithmic spiral motion, and L is a random value between −1 and 1.

It is important to mention that the selection between the declining surrounding strategy and the spiral position update is equally probable.

Search for prey

The search for prey, representing the exploration stage of WOA, can be achieved by adjusting the vector $\overrightarrow{A}$. This mechanism facilitates a global search by setting the absolute value of the vector $\overrightarrow{A}$ to $\left|\overrightarrow{A}\right|>1$. Mathematically, this stage can be formulated as Eqs. (5) and (6): (5)${\displaystyle \overrightarrow{D}=\left|\overrightarrow{C}\odot {\overrightarrow{X}}_{rand}-\overrightarrow{X}\right|}$ (6)${\displaystyle \overrightarrow{X}\left(t+1\right)={\overrightarrow{X}}_{rand}-\overrightarrow{A}\odot \overrightarrow{D}}$

where ${\overrightarrow{X}}_{rand}$ denotes the position vector of an indiscriminately chosen solution. It is important to note that the WOA method relies on two main parameters, $\overrightarrow{A}$ and $\overrightarrow{C}$, which need to be tuned.

Challenges of WOA

In practical applications, we encounter optimization problems with diverse behaviors and levels of complexity. Therefore, researchers strive to find an algorithm that is robust, requires minimal parameter tuning, and offers simplicity and fast convergence speed (Talbi, 2009). Real-world problems often involve shifted functions, where the global optimal solutions do not reside at the origin of coordinates and vary across dimensions. It is well-documented in the literature that many algorithms exhibit reduced performance for shifted functions (Liang, Qu & Suganthan, 2013), which necessitates appropriate modifications.

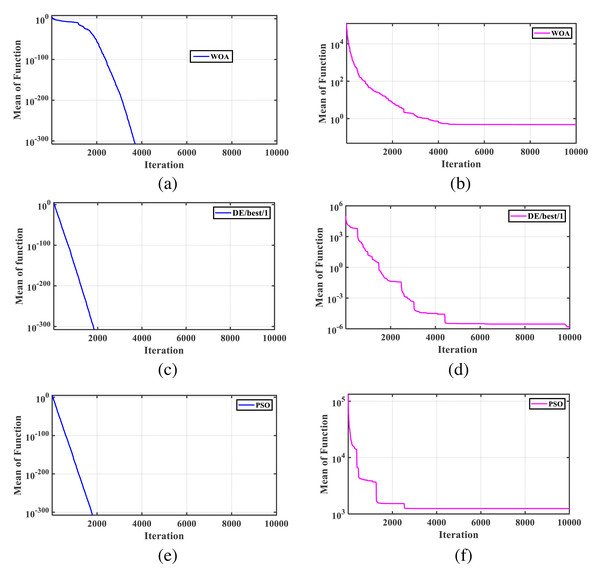
To investigate this issue with WOA, we conducted experiments using the conventional model of the sphere function (Mirjalili & Lewis, 2016) and its shifted counterpart, known as the Shifted Sphere Function (Suganthan et al., 2005). We aimed to determine the optimal solutions for these functions with 30 dimensions using WOA, PSO, and DE methods. Each function was independently evaluated in 25 runs, with 300,000 function evaluations (Suganthan et al., 2005) and a population size of 30 for the algorithm. The mean values obtained by WOA for the optimal response of the traditional sphere function and the shifted sphere function were 0 and 0.478, respectively. Figure 1 illustrates the convergence characteristics of WOA, DE/best/1, and PSO algorithms for both functions. It is worth noting that all algorithm parameters were set according to the recommendations in the original codes, leading to improved average performance across a wide range of problems. From the figure, it is evident that the original WOA exhibits reduced performance for shifted functions. Therefore, it is crucial to either tune the key controlling parameters or modify the WOA formulation to enhance its efficiency in solving a wider range of engineering and real-world problems.

Another issue with the original WOA is that it only stores the best solution among the entire population in each iteration. In contrast, algorithms like particle swarm optimization (PSO) store the personal best position (Pbest) for each member in each iteration, which enables directing the population members to avoid local optima. Therefore, an enhanced hybrid model of WOA can be developed by leveraging the advantageous features of other algorithms as an auxiliary operator. In this study, we present a new efficient hybrid variant of WOA that incorporates the formulations of PSO (Eberhart & Kennedy, 1995) and differential evolution (DE) (Storn & Price, 1997). This hybrid variant will be discussed in detail in the next section.

Pbest-guided differential WOA

The storage of only the best solution in WOA, similar to GA, is identified as a fundamental weakness of the algorithm based on our investigation. This limitation arises from eliminating many candidate solutions in each iteration, which could potentially be useful in subsequent iterations and enhance the algorithm’s optimization capability, as observed in DE and PSO algorithms. Consequently, we can leverage the models/formulations of basic DE, PSO, and their advanced variants, which have gained significant popularity in recent years, to enhance WOA’s performance in locating the global optimum of real-world optimization problems.

PSO-based Modification: The first modification proposed in this study involves storing the personal best(Pbest) position of each member in each iteration, denoted by →Xpbest > 1, similar to the PSO algorithm. With this Pbest-guided modification, the search equations can be rewritten as Eqs. (7)–(14): (7)${\displaystyle \overrightarrow{A}=2a.\overrightarrow{r}-a}$ (8)${\displaystyle \overrightarrow{C}=2\overrightarrow{r}}$ (9)${\displaystyle \overrightarrow{D}=\left|\overrightarrow{C}\odot {\overrightarrow{X}}_{Leader}\left(t\right)-\overrightarrow{Xpbest}\left(t\right)\right|}$ (10)${\displaystyle \overrightarrow{X}\left(t+1\right)={\overrightarrow{X}}_{Leader}\left(t\right)-\overrightarrow{A}\odot \overrightarrow{D}}$ (11)${\displaystyle \overrightarrow{D^{″}}=\left|\overrightarrow{C}\odot {\overrightarrow{X}}_{rand}-\overrightarrow{Xpbest}\right|}$ (12)${\displaystyle \overrightarrow{X}\left(t+1\right)={\overrightarrow{X}}_{rand}-\overrightarrow{A}\odot {\overrightarrow{D}}^{″}}$ (13)${\displaystyle \overrightarrow{D^{\prime }}=\left|{\overrightarrow{X}}_{Leader}-\overrightarrow{Xpbest}\right|}$ (14)${\displaystyle \overrightarrow{X}\left(t+1\right)={\overrightarrow{X}}_{Leader}\left(t\right)+\overrightarrow{D^{\prime }}.e^{BL}.Cos\left(2\pi L\right)}$

where Eqs. (9) and (10) denote the encircling prey phase, Eqs. (11) and (12) model the search for prey phase, and Eqs. (13) and (14) demonstrate the spiral position update. Note that in the proposed algorithm, the same as PSO, for each member of the population in each iteration, $\overrightarrow{Xpbest}$ is updated for each individual as Eq. (15): (15)${\displaystyle \overrightarrow{Xpbest}\left(t+1\right)=\left\{\begin{array}{c}\overrightarrow{X}\left(t+1\right);\begin{array}{c}\hfill \end{array}iff\left(\overrightarrow{X}\left(t+1\right)\right)\le f\left(\overrightarrow{Xpbest}\left(t\right)\right)\hfill \\ \overrightarrow{Xpbest}\left(t\right);\begin{array}{c}\hfill \end{array}else\hfill \end{array}\right.}$

DE-based modification: In the DE-based modification, we incorporate the best position found by each individual in all previous iterations. This enables us to leverage the mutations proposed in the DE algorithm to effectively enhance the original WOA. Therefore, in the second stage of the modification, a mutation phase, as defined in Eq. (16), is added to the formulation of WOA immediately after the main phases of the algorithm: (16)${\displaystyle \begin{array}{c}\overrightarrow{V}\left(t\right)=\overrightarrow{Xpbest}\left(t\right)+rand1\left({\overrightarrow{X}}_{Leader}\left(t\right)-\overrightarrow{Xpbest}\left(t\right)\right)\hfill \\ +rand2\left(\overrightarrow{Xpbes{t}_{r1}}\left(t\right)-\overrightarrow{Xpbes{t}_{r2}}\left(t\right)\right)\hfill \end{array}}$

where $\overrightarrow{Xpbes{t}_{r1}}$ and $\overrightarrow{Xpbes{t}_{r2}}$ are the personal best positions of two solutions randomly chosen from the population for updating each solution. Similarly, rand1 and rand2 are random vectors with dimensions equal to D (problem’s dimension), where the elements’ values range between 0 and 1. Subsequently, a random variable randj is generated for each dimension j of each solution, leading to Eq. (17): (17)${\displaystyle \overrightarrow{X_j}\left(t+1\right)=\left\{\begin{array}{c}{\overrightarrow{V}}_j\left(t\right)ifrandj>Cr\hfill \\ \hfill \\ \overrightarrow{X_j}\left(t\right)\text{otherwise}\hfill \end{array}.\right.}$

Here, Cr represents a control parameter, similar to the crossover rate used in evolutionary algorithms.

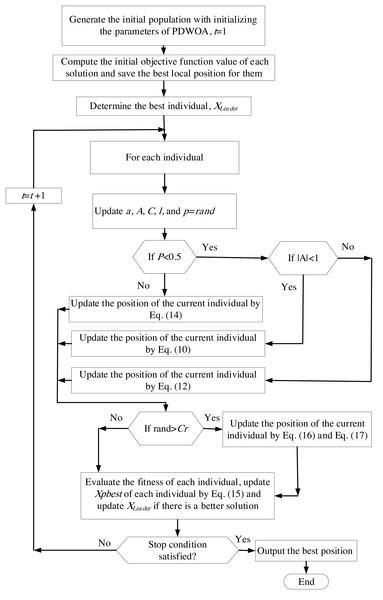
Finally, we want to emphasize that we employed the penalty method, a widely-used approach for addressing constraints in constrained optimization problems, in our research. The penalty method utilizes penalty functions to guide the optimization algorithm towards feasible solutions while penalizing infeasible solutions. To provide a visual representation of the proposed approach, we have included a flowchart of the Pbest-guided differential Whale Optimization Algorithm (PDWOA) in Fig. 2.

Solving CEC 2014 test functions using PDWOA

In order to compare the performance of PDWOA with that of the original WOA, 30 test functions with 30 dimensions have been selected from CEC 2014 Test Functions (Liang, Qu & Suganthan, 2013). These functions include unimodal (F1-F3), multimodal (F4-F16), hybrid (F17-F22), and composition (F23-F30) functions. For both algorithms, we consider a population number equal to 30 and iteration numbers equal to 10,000, i.e., the number of function evaluations (NFEs) done by each algorithm (for each test function) is 300,000. To find the optimal solution of each function, 25 separate runs have been executed for each algorithm and then, statistical analysis has been performed on the results.

A comparative study between DE, PSO, the original WOA, and the proposed PDWOA with three different Cr settings, i.e., a random value and the fixed values of 0.1 and 0.9, is presented in Table 1. In this table, the terms “Mean” and “Std”. represent the average value and standard deviation, respectively, of the results obtained from 25 independent runs for optimizing each function using each algorithm. The term “Rank” indicates the ranking of the algorithm’s Mean index, reflecting its effectiveness in optimizing the considered function. Additionally, “NB” represents the number of functions for which the algorithm achieves the best Mean index, while “MR” represents the mean of the Rank indices of the algorithm across all functions. It is evident from the table that the proposed algorithms, with two different Cr tunings, outperform the original algorithm significantly. Specifically, the PDWOA with Cr set to a random value and 0.1 surpasses the performance of the original WOA for 21 and 24 shifted test functions, respectively. Notably, even in cases where the suggested algorithm exhibits worse performance, the resulting outcomes do not deviate significantly from those obtained by the original WOA.

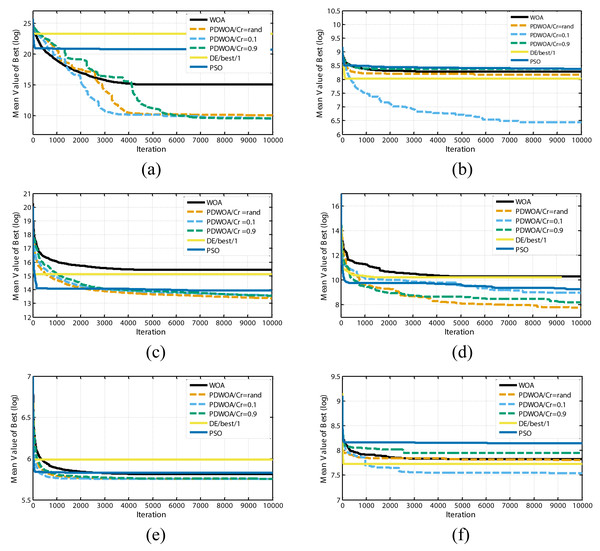
It can be further seen from results in Table 1 the suggested PDWOA could attain results of a much higher quality for test functions F1, F2, F3, F7, F10, F17, F18, F20, and F30 compared to the original algorithm. Furthermore, the convergence characteristics of the algorithms for some of the test functions are depicted in Fig. 3, which confirms the higher performance and convergence rate of the suggested PDWOA.

Table 2 presents the average simulation time of 25 runs for each of the CEC 2014 test functions, with the aim of comparing the computational burden of the proposed PDWOA to that of the original WOA, PSO, and DE algorithms. It is important to note that, due to the small difference in computational burden between different versions of PDWOA, only the simulation times of PDWOA/Cr = rand are reported in this table. The results indicate that, for 29 and 25 out of 30 test functions, PDWOA has lower mean simulation times than DE and PSO algorithms, respectively. However, for 24 out of 30 test functions, PDWOA has higher mean simulation times than the original WOA. Nonetheless, the maximum increase in mean simulation times by using the proposed improved version of WOA is only about 8%, occurring for test function 1. This increase is not too high considering the degree of improvement in the final solutions.

Table 3 displays a comparative analysis of the performance of the selected variant of the proposed Pbest-guided differential Whale Optimization Algorithm (i.e., PDWOA/Cr = rand) and several other state-of-the-art methods, including Arithmetic Optimization Algorithm (AOA) (Abualigah et al., 2021), Hierarchical Multi-swarm Cooperative TLBO (HMCTLBO) (Zou et al., 2017), Moth-Flame Optimization algorithm (MFO) (Mirjalili, 2015), Adaptive Weighted Particle Swarm Optimizer (AWPSO) (Liu et al., 2021), Gaussian bare-bones gradient-based optimization (GOMGBO) (Qiao et al., 2022), and Lévy flight Jaya Algorithm (LJA) (Iacca, dos Santos Junior & Veloso de Melo, 2021), for solving CEC 2014 test functions.

In this table, the symbols ‘=’, ‘−’, and ‘+’ are used to indicate the comparison between the method under consideration and the proposed PDWOA. The symbol ‘=’ represents an equal result, ‘−’ indicates that the method performs worse than the proposed PDWOA, and ‘+’ signifies that the method performs better than the proposed PDWOA. Furthermore, Nw, Nb, and Ne represent the number of times the considered method performs worse than, better than, or equal to the proposed PDWOA, respectively. The table presents a comprehensive comparison of the results achieved by PDWOA in relation to the benchmarked algorithms, shedding light on the efficacy and competitiveness of PDWOA in addressing the CEC 2014 test functions.

Statistical analysis

In this subsection, we present the results of two non-parametric statistical tests conducted to assess the performance of the proposed improved versions of the whale optimization algorithm (WOA), namely “PDWOA/Cr = rand”, “PDWOA/Cr = 0.1’, and “PDWOA/Cr = 0.9’. The tests include the Wilcoxon signed-rank test and the Friedman test, which provide insights into the algorithm rankings and pairwise comparisons.

The Friedman test was used to rank the algorithms based on their mean performance across all benchmark functions. The results of the Friedman test are presented in Table 4. In this table, the mean rank index represents the average of the Rank indices of each algorithm for all test functions, while the RankT index shows the rank of each algorithm in the list of sorted mean rank indices. Specifically, PDWOA/Cr = rand achieved the best performance with the lowest mean rank of 3.0167, followed by PDWOA/Cr = 0.1 (mean rank: 3.9), PSO (mean rank: 5.9), and PDWOA/Cr = 0.9 (mean rank: 5.9667).

Additionally, the results of the Wilcoxon signed-rank test with a significance level of 0.05 are presented in Table 5, showing the p-values and confidence intervals for pairwise comparisons between PDWOA/Cr = rand and other algorithms. In this table, SoPR and SoNR represent the combined positive and negative ranks. Similarly, MoPR and MoNR represent the average positive and negative ranks, respectively. The notation F(i)<F(j) indicates how many times the first algorithm performs better than the second one, while F(j)<F(i) signifies the opposite scenario. It’s important to highlight that in the Wilcoxon test, positive ranks correspond to cases where the first algorithm surpasses the second one. The test results reveal statistically significant differences in performance between PDWOA/Cr = rand and several other algorithms.

PDWOA/Cr = rand was found to have significantly better performance compared to DE/rand/1, PSO, WOA, PDWOA/Cr = 0.9, AOA, AWPSO, GOMGBO, MFO, and LJA, as indicated by the low p-values obtained. The confidence intervals further support this finding, showing that PDWOA/Cr = rand consistently outperformed these algorithms over a wide range of objective function values.

However, when comparing PDWOA/Cr = rand with PDWOA/Cr = 0.1, the obtained p-value (0.0661) suggests that the difference in performance between these two algorithms is not statistically significant at the 0.05 significance level. It is worth noting that PDWOA/Cr = rand still exhibits a slightly better performance trend.

Overall, the results of the statistical tests support the superiority of PDWOA/Cr = rand compared to the other algorithms tested. It demonstrates consistent and competitive performance, as evidenced by its lower mean rank in the Friedman test and its significant performance advantages in the pairwise comparisons based on the Wilcoxon signed-rank test.

PDWOA for solving constrained engineering optimization

So as to further demonstrate the optimization power of the suggested algorithm, we have selected three renowned engineering problems and solved them with the proposed method. To solve these problems, the population sizes selected for each algorithm is 60 and the number of iterations of each algorithm for each run is 1,000. For each problem, optimization was performed in 30 independent runs. All parameters of the algorithms used here are exactly according to the main references suggested by the algorithm designers.

Pressure vessel optimal design (engineering problem 1)

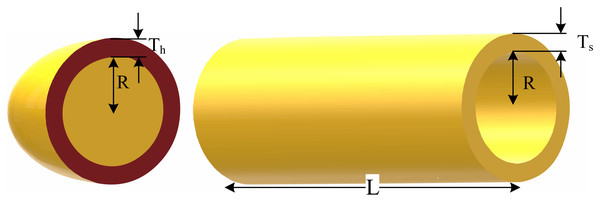
The problem is focused on optimally finding two discrete (x₁ and x₂) and two continuous (x₃ and x₄) decision variables for the minimization of the cost of a pressure vessel (Fig. 4) subject to three linear and one nonlinear inequality constraint. The optimization variables are the thickness of the shell (x₁ or T_s), the thickness of the head (x₂ or T_h), the inner radius (x₃ or R), and the length of the cylindrical part of the vessel (x₄ or L) (Askarzadeh, 2016).

Minimize: (18)${\displaystyle f\left(X\right)=0.6224x_1{x}_3{x}_4+1.7781x_2{x}_3^2+3.1661x_1^2{x}_4+19.84x_1^2{x}_3}$

subject to: (19)${\displaystyle g_1\left(X\right)=-x_1+0.0193x_3\le 0,}$ (20)${\displaystyle g_2\left(X\right)=-x_2+0.00954x_3\le 0,}$ (21)${\displaystyle g_3\left(X\right)=-\pi x_3^2{x}_4-\frac{4}{3}\pi x_3^3+1,296,000\le 0,}$ (22)${\displaystyle g_4\left(X\right)=x_4-240\le 0,}$

where x₁, x₂ ∈ [0, 100], and x₃, x₄ ∈ [10, 200].

Table 6 presents the results of PDWOA in solving this problem compared to several new algorithms, including quantum-behaved PSO (QPSO) (Coelho L dos, dos Santos Coelho & Coelho L dos, 2010), ABC (Akay & Karaboga, 2012), GA enhanced with dominance-based tournament selection (GA4) (Coello Coello et al., 2002), co-evolutionary PSO (CPSO) (He & Wang, 2007), co-evolutionary DE (CDE) (Huang, Wang & He, 2007), gaussian quantum-behaved PSO (G-QPSO) (Coelho L dos, dos Santos Coelho & Coelho L dos, 2010), Unified PSO (UPSO) (Parsopoulos & Vrahatis, 2005), Crow search algorithm (CSA) (Askarzadeh, 2016), hybrid GA and artificial immune system (HAIS-GA) (Coello & Cortés, 2004), bacterial foraging optimization algorithm (BFOA) (Mezura-Montes & Hernández-Ocana, 2008), evolution strategies (ES) (Mezura-Montes & Coello, 2008), modified T-Cell Algorithm (Aragón, Esquivel & Coello, 2010), GA enhanced with self-adaptive penalty approach (GA3) (Coello Coello, 2000), Queuing search (QS) algorithm (Zhang et al., 2018), and automatic dynamic penalization (ADP) for GA (BIANCA) (Montemurro, Vincenti & Vannucci, 2013), K-means optimizer (KO) (Minh et al., 2022), and termite life cycle optimizer (TLCO) (Minh et al., 2023b; Minh et al., 2023a). The best solutions for the considered problem found using the original and proposed versions of WOA are presented in Table 7. The results demonstrate the effectiveness of the proposed PDWOA in achieving high-quality solutions for the optimization problem.

Table 6:

Best statistical results of various algorithms for engineering problem 1.

Methods	Best	Mean	Worst	Std.
QPSO (Coelho L dos, dos Santos Coelho & Coelho L dos, 2010)	6059.7209	6440.3786	8017.2816	479.2671
ABC (Akay & Karaboga, 2012)	6059.714339	6245.308144	N.A.	2.05e+02
GA4 (Coello Coello et al., 2002)	6059.9463	6177.2533	6469.3220	130.9297
CPSO (He & Wang, 2007)	6061.0777	6147.1332	6363.8041	86.4545
CDE (Huang, Wang & He, 2007)	6059.7340	6085.2303	6371.0455	43.013
G-QPSO (Coelho L dos, dos Santos Coelho & Coelho L dos, 2010)	6059.7208	6440.3786	7544.4925	448.4711
UPSO (Parsopoulos & Vrahatis, 2005)	6154.70	8016.37	9387.77	745.869
ES (Mezura-Montes & Coello, 2008)	6059.746	6850.00	7332.87	426
T-Cell (Aragón, Esquivel & Coello, 2010)	6390.554	6737.065	7694.066	357
GA3 (Coello Coello, 2000)	6288.7445	6293.8432	6308.4970	7.4133
HAIS-GA (Coello & Cortés, 2004)	6832.584	7187.314	8012.615	276
CSA (Askarzadeh, 2016)	6059.71436343	6342.49910551	7332.84162110	384.94541634
BFOA (Mezura-Montes & Hernández-Ocana, 2008)	6060.460	6074.625	N.A.	156
BIANCA (Montemurro, Vincenti & Vannucci, 2013)	6059.9384	6182.0022	6447.3251	122.3256
QS (Zhang et al., 2018)	6059.714	6060.947	6090.526	N.A.
KO	6059.71475731827	6059.72453197228	N.A.	0.005942
TLCO	6059.71433504844	N.A.	N.A.	N.A.
WOA	6059. 823537	6115.250471	6314.025148	62.35
PDWOA/Cr= 0.9	6059.714335	6064.922632	6084.003815	12.94
PDWOA/Cr= rand	6059.714335	6063.175326	6090.742650	24.65
PDWOA/Cr= 0.1	6059.714335	6060.789025	6064.324186	1.83

DOI: 10.7717/peerjcs.1557/table-6

Table 7:

The best solutions for engineering problem 1.

Design variables	WOA	PDWOA/Cr= 0.9	PDWOA/Cr= rand	PDWOA/Cr= 0.1
x1	0.8125	0.8125	0.8125	0.8125
x2	0.4375	0.4375	0.4375	0.4375
x3	42.09765834	42.09844559	42.09844559	42.09844559
x4	176.6469213	176.63659592	176.63659592	176.63659592
g1(X)	−1.519403799987718e−05	−1.130000537585829e−10	−1.130000537585829e−10	−1.130000537585829e−10
g2(X)	−0.0358883394364	−0.035880829071400	−0.035880829071400	−0.035880829071400
g3(X)	−3.172713808366098	−2.788752317428589e−05	−2.788752317428589e−05	−2.788752317428589e−05
g4(X)	−63.353078699999998	−63.363404080000009	−63.363404080000009	−63.363404080000009
Best	6059. 823537	6059.714335	6059.714335	6059.714335

DOI: 10.7717/peerjcs.1557/table-7

Tension/compression spring optimal design (engineering problem 2)

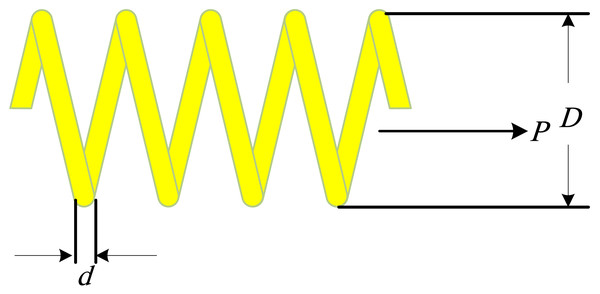
The problem involves finding three continuous decision variables to minimize the weight of the spring (Fig. 5). The optimization variables are the wire diameter (d or x₁), mean coil diameter (D or x₂), and the number of active coils (P or x₃), subject to one linear and three nonlinear inequality constraints (Askarzadeh, 2016).

Minimize: (23)${\displaystyle f\left(X\right)=\left(x_3+2\right)x_2{x}_1^2}$

subject to: (24)${\displaystyle g_1\left(X\right)=1-\frac{x_2^3{x}_3}{71,785x_1^4}\le 0,}$ (25)${\displaystyle g_2\left(X\right)=\frac{4x_2^2-x_1{x}_2}{12,566\left(x_1^3{x}_2-x_1^4\right)}+\frac{1}{5,108x_1^2}-1\le 0,x_3\in \left[2,15\right]}$ (26)${\displaystyle g_3\left(X\right)=1-\frac{140.45x_1}{x_2^2{x}_3}\le 0,}$ (27)${\displaystyle g_4\left(X\right)=\frac{x_1+x_2}{1.5}-1\le 0.}$ In which x₁ ∈ [0.05, 2], x₂ ∈ [0.25, 1.3], and x₂ ∈ [2, 15].

Table 8 compares the results of the proposed method for solving the engineering problem 2 with several other algorithms, including BFOA (Mezura-Montes & Hernández-Ocana, 2008), T-Cell (Aragón, Esquivel & Coello, 2010), CDE (Huang, Wang & He, 2007), CPSO (He & Wang, 2007), a cultural algorithm (CA) (Coello Coello & Becerra, 2004), GA4 (Coello Coello et al., 2002), GA3 (Coello Coello, 2000), TEO (Kaveh & Dadras, 2017), G-QPSO (Coelho L dos, dos Santos Coelho & Coelho L dos, 2010), SBO (Ray & Liew, 2003), evolutionary algorithms ((l + k)-ES) (Mezura-Montes & Coello, 2005), UPSO (Parsopoulos & Vrahatis, 2005), Grey wolf optimizer (GWO) (Mirjalili, Mirjalili & Lewis, 2014), SDO (Zhao, Wang & Zhang, 2019), QS (Zhang et al., 2018), Water cycle algorithm (WCA) (Eskandar et al., 2012), BIANCA (Montemurro, Vincenti & Vannucci, 2013), KO (Minh et al., 2022), TLCO (Minh et al., 2023b; Minh et al., 2023a), planet optimization algorithm (POA) (Sang-To et al., 2022), Cuckoo Search Algorithm (CS) (Cuong-Le et al., 2021), and the new movement strategy of cuckoo search (NMS-CS) (Cuong-Le et al., 2021). Table 9 provides the best solutions obtained by the original and proposed versions of WOA for this problem. The findings indicate that the suggested PDWOA is successful in attaining excellent solutions for the optimization issue.

Table 8:

Best statistical results of various algorithms for engineering problem 2.

Methods	Best	Mean	Worst	Std.
CA (Coello Coello & Becerra, 2004)	0.012721	0.013568	0.0151156	8.4e−04
BFOA (Mezura-Montes & Hernández-Ocana, 2008)	0.012671	0.012759	N.A.	1.36e−04
T-Cell (Aragón, Esquivel & Coello, 2010)	0.012665	0.012732	0.013309	9.4e−05
CDE (Huang, Wang & He, 2007)	0.012670	0.012703	0.012790	2.07e−05
CPSO (He & Wang, 2007)	0.0126747	0.012730	0.012924	5.19e−05
TEO (Kaveh & Dadras, 2017)	0.012665	0.012685	0.012715	4.4079e−06
G-QPSO (Coelho L dos, dos Santos Coelho & Coelho L dos, 2010)	0.012665	0.013524	0.017759	1.268e−03
SBO (Ray & Liew, 2003)	0.012669249	0.012922669	0.016717272	5.92e−04
GA4 (Coello Coello et al., 2002)	0.012681	0.012742	0.012973	9.5e−05
GA3 (Coello Coello, 2000)	0.0127048	0.012769	0.012822	3.93e−05
(l + k)-ES (Mezura-Montes & Coello, 2005)	0.012689	0.013165	N.A.	3.9e−04
UPSO (Parsopoulos & Vrahatis, 2005)	0.01312	0.02294	N.A.	7.2e−03
GWO (Mirjalili, Mirjalili & Lewis, 2014)	0.0126660	N.A.	N.A.	N.A.
WCA (Eskandar et al., 2012)	0.012665	0.012746	0.012952	8.06e−05
BIANCA (Montemurro, Vincenti & Vannucci, 2013)	0.012671	0.012681	0.012913	5.1232e−05
SDO (Zhao, Wang & Zhang, 2019)	0.0126663	0.0126724	0.0126828	6.1899e−06
QS (Zhang et al., 2018)	0.012665	0.012666	0.012669	N.A.
KO	0.012665994	0.012917292	N.A.	0.00030139
TLCO	0.0126652328	N.A.	N.A.	N.A.
POA	0.01266588	N.A.	N.A.	N.A.
CS	0.012665871	N.A.	N.A.	N.A.
NMS-CS	0.012665233	N.A.	N.A.	N.A.
WOA	0.012667	0.013586	0.018416	5.05e−03
PDWOA/Cr= 0.9	0.012665	0.012695	0.012842	8.75e−06
PDWOA/Cr= rand	0.012665	0.012706	0.012907	1.18e−05
PDWOA/Cr= 0.1	0.012665	0.012665	0.012666	9.22e−08

DOI: 10.7717/peerjcs.1557/table-8

Table 9:

The best solutions for engineering problem 2.

Design variables	WOA	PDWOA/Cr= 0.9	PDWOA/Cr= rand	PDWOA/Cr= 0.1
x1	0.0517315934	0.0515902788	0.0516488707	0.0516911532
x2	0.3577231396	0.3543444741	0.3557507777	0.3567674033
x3	11.2318481822	11.4295493851	11.3460406066	11.2862994555
g1(X)	−8.105263015556474e−05	−2.067013876949631e−06	−1.124305991995200e−05	−1.953083625561014e−05
g2(X)	−4.202663105634663e−05	−3.336199576375876e−06	−1.936754291387288e−06	−1.509602815197297e−06
g3(X)	−4.055129747949155	−4.049044297898749	−4.051804364878148	−4.053776839282882
g4(X)	−0.727030178	−0.729376831400	−0.7284002344	−0.727694295666667
Best	0.012667	0.012665	0.012665	0.012665

DOI: 10.7717/peerjcs.1557/table-9

Welded beam optimal design (engineering problem 3)

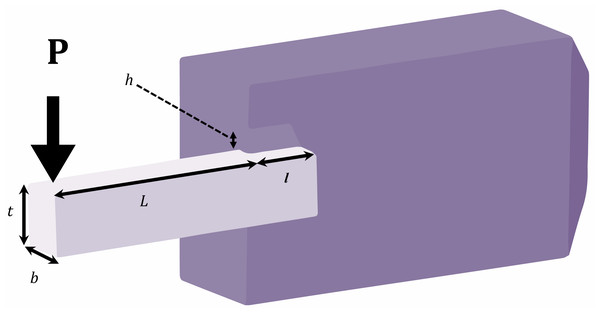
The problem is focused on optimally finding four continuous decision variables for minimizing the cost of a welded beam (Fig. 6) subject to two linear and five nonlinear inequality constraints. The optimization variables are x₁ or h, x₂ or l, x₃ or t, and x₄ or b (Askarzadeh, 2016).

Minimize: (28)${\displaystyle f\left(X\right)=1.10471x_2{x}_1^2+0.04811x_3{x}_4\left(14+x_2\right)}$

subject to: (29)${\displaystyle g_1\left(X\right)=\tau \left(x\right)-{\tau }_{\max }\le 0,}$ (30)${\displaystyle g_2\left(X\right)=\sigma \left(x\right)-{\sigma }_{\max }\le 0,}$ (31)${\displaystyle g_3\left(X\right)=x_1-x_4\le 0,}$ (32)${\displaystyle g_4\left(X\right)=0.10471x_1^2+0.04811x_3{x}_4\left(14+x_2\right)-5\le 0.}$ (33)${\displaystyle g_5\left(X\right)=0.125-x_1\le 0,}$ (34)${\displaystyle g_6\left(X\right)=\delta \left(x\right)-{\delta }_{\max }\le 0,}$ (35)${\displaystyle g_7\left(X\right)=P-P_c\left(x\right)\le 0,}$ (36)${\displaystyle \tau \left(x\right)=\sqrt{{\left({\tau }^{{}^{\prime }}\right)}^2+2{\tau }^{{}^{\prime }}{\tau }^{\prime \prime }\frac{x_2}{2R}+{\left({\tau }^{\prime \prime }\right)}^2}}$ (37-38)${\displaystyle {\tau }^{{}^{\prime }}=\frac{P}{\sqrt{2}{x}_1{x}_2},{\tau }^{\prime \prime }=\frac{MR}{J},}$ (39-41)${\displaystyle M=P\left(L+\frac{x_2}{2}\right),R=\sqrt{\frac{x_2^2}{4}+{\left(\frac{x_1+x_3}{2}\right)}^2},\delta \left(x\right)=\frac{4P{L}^3}{E{x}_3^3{x}_4}}$ (42-43)${\displaystyle J=2\left[\sqrt{2}{x}_1{x}_2\left\{\frac{x_2^2}{12}+{\left(\frac{x_1+x_3}{2}\right)}^2\right\}\right],\sigma \left(x\right)=\frac{6PL}{x_4{x}_3^2},}$ (44)${\displaystyle P_c\left(x\right)=\frac{4.013E\sqrt{\frac{x_4^6{x}_3^2}{36}}}{L^2}\left(1-\frac{x_3}{2L}\sqrt{\frac{E}{4G}}\right),}$

where P = 6,000 lb; L = 14 in; E = 30e6 psi; G = 12e6 psi; τ_max =13,000 psi; σ_max =30,000 psi; δ_max = 0.25 in; x₁ ∈ [0.1, 2]; x₂ ∈ [0.1, 10]; x₃ ∈ [0.1, 10]; and x₄ ∈ [0.1, 2].

Table 10 presents the results of the proposed method for solving the engineering problem 3 in comparison to several other algorithms, including a cooperative PSO with stochastic movements (EPSO) (Ngo, Sadollah & Kim, 2016), BFOA (Mezura-Montes & Hernández-Ocana, 2008), T-Cell Algorithm (Aragón, Esquivel & Coello, 2010), CDE (Huang, Wang & He, 2007), CPSO (He & Wang, 2007), Derivative-Free Filter Simulated Annealing Method (FSA) (Hedar & Fukushima, 2006), TEO (Kaveh & Dadras, 2017), SBO (Ray & Liew, 2003), GA4 (Coello Coello et al., 2002), (l + k)-ES (Mezura-Montes & Coello, 2005), UPSO (Parsopoulos & Vrahatis, 2005), GWO (Mirjalili, Mirjalili & Lewis, 2014), SFO (Shadravan, Naji & Bardsiri, 2019), HGSO (Hashim et al., 2019), WCA (Eskandar et al., 2012), BIANCA (Montemurro, Vincenti & Vannucci, 2013), SBO (Ray & Liew, 2003), KO (Minh et al., 2022), TLCO (Minh et al., 2023b; Minh et al., 2023a), POA (Sang-To et al., 2022), CS (Cuong-Le et al., 2021), and NMS-CS (Cuong-Le et al., 2021). Table 11 presents the best solutions found by the original and proposed versions of WOA for this problem. The outcomes exhibit the efficacy of the suggested PDWOA in attaining top-notch solutions for the optimization issue.

Table 10:

Best statistical results of various algorithms for engineering problem 3.

Methods	Best	Mean	Worst	Std.
EPSO (Ngo, Sadollah & Kim, 2016)	1.7248530	1.7282190	1.7472200	5.62e−03
BFOA (Mezura-Montes & Hernández-Ocana, 2008)	2.3868	2.4040	N.A.	1.6e−02
T-Cell (Aragón, Esquivel & Coello, 2010)	2.3811	2.4398	2.7104	9.314e−02
CDE (Huang, Wang & He, 2007)	1.73346	1.768158	1.824105	2.2194e−02
CPSO (He & Wang, 2007)	1.728024	1.748831	1.782143	1.2926e−02
FSA (Hedar & Fukushima, 2006)	2.3811	2.4041	2.4889	N.A.
TEO (Kaveh & Dadras, 2017)	1.725284	1.768040	1.931161	5.81661e−02
SBO (Ray & Liew, 2003)	2.3854347	3.0025883	6.3996785	9.59e−01
GA4 (Coello Coello et al., 2002)	1.728226	1.792654	1.993408	7.47e−02
(l + k)-ES (Mezura-Montes & Coello, 2005)	1.724852	1.777692	N.A.	8.8e−02
UPSO (Parsopoulos & Vrahatis, 2005)	1.92199	2.83721	N.A.	6.83e−01
GWO (Mirjalili, Mirjalili & Lewis, 2014)	1.72624	N.A.	N.A.	N.A.
SFO (Shadravan, Naji & Bardsiri, 2019)	1.73231	N.A.	N.A.	N.A.
HGSO (Hashim et al., 2019)	1.7260	1.7265	1.7325	7.66e−03
WCA (Eskandar et al., 2012)	1.724856	1.726427	1.744697	4.29e−03
BIANCA (Montemurro, Vincenti & Vannucci, 2013)	1.725436	1.752201	1.793233	2.3001e−02
KO	1.725344872	1.75727933	N.A.	0.029125
TLCO	1.724852433	N.A.	N.A.	N.A.
POA	1.72564	N.A.	N.A.	N.A.
CS	1.73139841	N.A.	N.A.	N.A.
NMS-CS	1.72620872	N.A.	N.A.	N.A.
WOA	1.7273929	2.2852435	3.2784166	2.62
PDWOA/Cr= 0.9	1.7248523	1.7310629	1.7491305	9.83e−04
PDWOA/Cr= rand	1.7248523	1.7588375	1.7709064	2.06e−03
PDWOA/Cr= 0.1	1.7248523	1.7259521	1.7340485	5.93e−05

DOI: 10.7717/peerjcs.1557/table-10

Table 11:

The best solutions for engineering problem 3.

Design variables	WOA	PDWOA/Cr= 0.9	PDWOA/Cr= rand	PDWOA/Cr= 0.1
x1	0.2053718352	0.2057296398	0.20572963980	0.20572963980
x2	3.4771582193	3.470488670	3.4704886655	3.4704886655
x3	9.0472014495	9.0366239108	9.0366239101	9.0366239101
x4	0.2057779509	0.2057296398	0.2057296398	0.2057296398
g1(X)	−9.453362733127506	−1.514258474344388e−05	−2.265333023387939e−07	−2.265333023387939e−07
g2(X)	−77.134747837790201	−4.967081622453407e−06	−3.193272277712822e−07	−3.193272277712822e−07
g3(X)	−4.061157000000149e−04	0.0	0.0	0.0
g4(X)	−3.43020541215535	−3.432983784788387	−3.432983785311915	−3.432983785311915
g5(X)	−0.08037183520	−0.08072963980	−0.080729639800	−0.080729639800
g6(X)	−0.235594362774535	−0.235540322587856	−0.235540322584496	−0.235540322584496
g7(X)	−8.845720840467948	−1.411061930411961e−06	−1.105492628994398e−06	−1.105492628994398e−06
Best	1.7273929	1.7248523	1.7248523	1.7248523

DOI: 10.7717/peerjcs.1557/table-11