Bayesian computation for the common coefficient of variation of delta-lognormal distributions with application to common rainfall dispersion in Thailand

Introduction

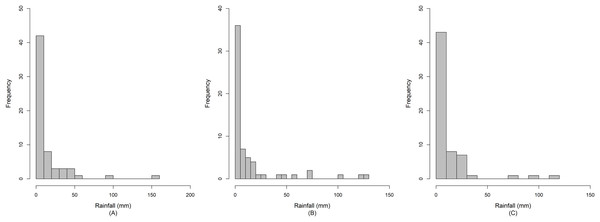
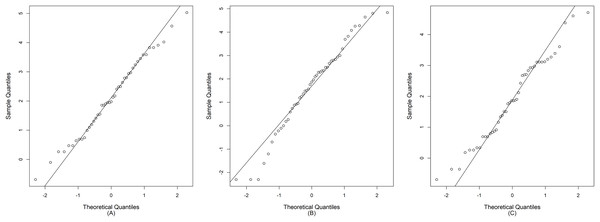
Currently, the anthropomorphic emissions of greenhouse gases, sulfate aerosols, and black carbon are having a seriously deleterious effect on the Earth’s climate (Nema, Nema & Roy, 2012). This phenomenon is directly increasing the global temperature, warming the oceans, and melting the polar ice caps, thereby causing a rise in sea level and initiating extreme weather events (NASA, 2020). Southeast Asia is a tropical area that is affected by ocean currents, prevailing winds, and abundant rainfall during the monsoon season (WorldAtlas, 2021). Thailand is located in Southeast Asia, where the climate is influenced by the monsoon winds. Especially, the combined effect of the southwest monsoon, the Inter-Tropical Convergence Zone, and tropical cyclones causes plenty of rain to fall over the country (Thai Meteorological Department, 2015). Large amounts of rainfall cause regular flooding in some areas of the country, thereby leading to damage to property and loss of life. Moreover, Thailand is an agricultural country, and rainfall fluctuation makes it difficult to predict heavy precipitation that may cause loss of or damage to crops. Therefore, it is necessary to measure the dispersion of rainfall in specific areas by using statistical tools such as the coefficient of variation (CV) to enable accurate prediction of future catastrophic events. Nan is a province in Thailand located near the origin of the Nan River that flows into the Chao Phraya River. Furthermore, throughout the year, the precipitation in Nan fluctuates between a precipitation deficit and heavy rainfall. The latter accompanied by thunderstorms occurs in the late summer period, and due to the southwest monsoon, the amount of daily rainfall increases from mid-May to early October with the highest daily rainfall frequently in August or September, which can cause flooding in some areas (Thai Meteorological Department, 2015). Therefore, datasets of daily rainfall from the three areas (Chiang Klang, Tha Wang Pha, and Pua) in Nan province in August 2018 and 2019 were selected. These data comprise positive values that conform to a lognormal distribution, and true zero values, in which the frequency conforms to a binomial distribution, as presented in Fig. 1. In addition, the normality plots shown in Fig. 2 together with the Akaike information criterion (AIC) and the Bayesian information criterion (BIC) indicate that the daily rainfall data from the three areas follow delta-lognormal distributions. Furthermore, many researchers have reported that rainfall data follow a delta-lognormal distribution (Fukuchi, 1988; Shimizu, 1993; Yue, 2000; Kong et al., 2012; Maneerat, Niwitpong & Niwitpong, 2019a, 2020a, 2020b; Yosboonruang, Niwitpong & Niwitpong, 2019b, 2020; Yosboonruang & Niwitpong, 2020).

Since the CV is the ratio of the mean and the standard deviation of a population, it is free from units of measurement and is often used to measure the dispersion of data and compare it between populations. For statistical inference, several methods for constructing confidence intervals for the CV and functions of the CV have been suggested (e.g. Pang et al., 2005; Hayter, 2015; Nam & Kwon, 2017; Yosboonruang, Niwitpong & Niwitpong, 2018, 2019a, 2019b, 2020; Yosboonruang & Niwitpong, 2020). However, since using the common CV of delta-lognormal distributions for statistical inference has not previously been reported, this has become our research interest as it is useful for measuring the dispersion in several independent data series, especially rainfall data.

Several statisticians have suggested confidence intervals for the common CV of normal and non-normal distributions. Once Gupta, Ramakrishnan & Zhou (1999) obtained the asymptotic variance of the common CV for normal distributions, they constructed confidence intervals and compared their coverage probabilities and expected lengths. Tian (2005) developed a method by using the concept of the generalized confidence interval (GCI) for the common CV. Subsequently, Behboodian & Jafari (2008) used the concept of generalized p-values and GCI to construct a new method and compared it with Tian’s method (Tian, 2005); the former outperformed the others by attaining a suitable coverage probability and the shortest expected length. Ng (2014) constructed confidence intervals for the common CV of lognormal distributions using the generalized variables approach; the performance of the proposed method was similar to Tian’s method (Tian, 2005). Liu & Xu (2015) constructed a confidence interval for the common CV of several normal populations based on the confidence distribution interval. Thangjai & Niwitpong (2017) proposed the adjusted method of variance estimates recovery (MOVER) to construct the confidence interval for the weighted CV of two-parameter exponential distributions; a performance comparison between it, GCI, and a large sample method revealed that GCI performed the best and adjusted MOVER was only suitable for data with positive values. Recently, Thangjai, Niwitpong & Niwitpong (2020a) applied adjusted GCI and a computational method to construct confidence intervals for the common CV of normal distributions; they compared them with GCI and the adjusted MOVER, the results of which show that the adjusted GCI is appropriate for small samples and the computational method was suitable for large ones. In addition, Thangjai, Niwitpong & Niwitpong (2020b) extended the computational approach and MOVER to produce confidence intervals for the common CV of lognormal distributions and compared their performances with those employing fiducial GCI (FGCI) and Bayesian approaches, of which FGCI was the best. Unfortunately, the work of Thangjai, Niwitpong & Niwitpong (2020b) considered only the positively skewed distribution: lognormal distribution. In this work, we regarded the lognormal distribution that contained true zero values, the delta-lognormal distribution, for the confidence interval construction of the common CV. Therefore, the research by Thangjai, Niwitpong & Niwitpong (2020b) also needs to continue as rainfall data must be the delta-lognormal distribution.

The fact that daily rainfall data can usually be fitted to a delta-lognormal distribution after collecting data over a sufficiently long period has drawn interest from several researchers to present statistical inference for its parameters. Several researchers have suggested confidence intervals for the mean and functions of the mean of delta-lognormal distributions, such as the traditional method, the normal algorithm, the exponential algorithm (Kvanli, Shen & Deng, 1998), bootstrapping, the likelihood ratio, the signed log-likelihood ratio (Zhou & Tu, 2000; Tian, 2005; Tian & Wu, 2006), GCI (Tian, 2005; Chen & Zhou, 2006; Li, Zhou & Tian, 2013; Wu & Hsieh, 2014; Hasan & Krishnamoorthy, 2018; Maneerat, Niwitpong & Niwitpong, 2018, 2019b), MOVER (Maneerat, Niwitpong & Niwitpong, 2018, 2019a, 2019b), Aitchison’s estimator, a modified Cox’s method, a modified Land’s method, the profile likelihood interval (Fletcher, 2008; Wu & Hsieh, 2014), FGCI (Li, Zhou & Tian, 2013; Hasan & Krishnamoorthy, 2018; Maneerat, Niwitpong & Niwitpong, 2019a), as well as Bayesian approaches (Maneerat, Niwitpong & Niwitpong, 2019a). Moreover, confidence interval estimations for the variance (Maneerat, Niwitpong & Niwitpong, 2020a, 2020b), CV (Yosboonruang, Niwitpong & Niwitpong, 2018, 2019a, 2019b), and functions of the CV (Yosboonruang & Niwitpong, 2020; Yosboonruang & Niwitpong, 2020) of delta-lognormal distributions have been suggested, including GCI, the modified Fletcher’s method, FGCI, MOVER, the Bayesian approach, and bootstrapping.

Herein, we construct confidence intervals for the common CV of delta-lognormal distributions based on FGCI, the Bayesian approach, and MOVER. Their performances were compared in terms of their coverage probabilities and expected lengths. The methods for the confidence intervals estimation are presented in the next section. Subsequently, the results and discussion of a simulation study are analyzed, followed by the use of daily rainfall data to determine their applicability in real situations. Finally, conclusions on the study are offered.

Methods

Let $X_{ij}$, $i=1,2,\dots ,k$, $j=1,2,\dots ,n_i$ be a random variable of size $n_i$ from $k$ delta-lognormal distributions with density function

(1) $$f\left(x_{ij};{\mu }_i,{\sigma }_i^2,{\delta }_i\right)=\left(1-{\delta }_i\right){\mathrm{I}}_0\left[x_{ij}\right]+{\delta }_i\frac{1}{x_{ij}\sqrt{2\pi }{\sigma }_i}\exp \left\{-\frac{1}{2}{\left[\frac{\ln \left(x_{ij}\right)-{\mu }_i}{{\sigma }_i}\right]}^2\right\}{\mathrm{I}}_{\left(0,\mathrm{\infty }\right)}\left[x_{ij}\right],$$where ${\mathrm{I}}_0\left[x_{ij}\right]$ is an indicator function for which the values are 1 when $x_{ij}=0$, and 0 otherwise; ${\mathrm{I}}_{\left(0,\mathrm{\infty }\right)}\left[x_{ij}\right]$ are equal to 0 and 1 when $x_{ij}=0$ and $x_{ij}>0$, respectively; and ${\delta }_i=P\left(X_{ij}>0\right)$. This distribution is a combination of lognormal and binomial distributions. The numbers of positive and zero observations are defined as $n_{i1}$ and $n_{i0}$, respectively, where $n_i=n_{i1}+n_{i0}$. According to Aitchison (1955), the mean and variance of a delta-lognormal distribution are defined as

(2) $$E\left(X_{ij}\right)={\delta }_i\exp \left({\mu }_i+\frac{{\sigma }_i^2}{2}\right)$$and

(3) $${\sigma }_i^2={\delta }_i\exp \left(2{\mu }_i+{\sigma }_i^2\right)\left[\exp \left({\sigma }_i^2\right)-{\delta }_i\right],$$respectively. Since the CV computed from ${\sigma }_i/{\mu }_i$, then

(4) $$CV(X_{ij})={\eta }_i={\left[\frac{\exp \left({\sigma }_i^2\right)-{\delta }_i}{{\delta }_i}\right]}^{\frac{1}{2}}.$$

By using the log-transformation (Yosboonruang, Niwitpong & Niwitpong, 2018), let

(5) $${\phi }_i=\frac{1}{2}\left\{\ln \left[\exp \left({\sigma }_i^2\right)-{\delta }_i\right]-\ln \left({\delta }_i\right)\right\}.$$

The unbiased estimators for ${\sigma }_i^2$ and ${\delta }_i$ are ${\hat{\sigma }}_i^2=\sum _{j=1}^{n_{i1}}{\left[\ln \left(x_{ij}\right)-{\hat{\mu }}_i\right]}^2/\left(n_{i1}-1\right)$ and ${\hat{\delta }}_i=n_{i1}/n_i$, for $i=1,2,\dots ,k$, where ${\hat{\mu }}_i=\sum _{j=1}^{n_{i1}}\ln \left(x_{ij}\right)/n_{i1}$, respectively, then

(6) $${\hat{\phi }}_i=\frac{1}{2}\left\{\ln \left[\exp \left({\hat{\sigma }}_i^2\right)-{\hat{\delta }}_i\right]-\ln \left({\hat{\delta }}_i\right)\right\}.$$

The approximately unbiased estimate variance of ${\hat{\phi }}_i$ is

(7) $$\hat{V}\left({\hat{\phi }}_i\right)\approx \frac{\left({\hat{b}}_i-{\hat{a}}_i\right)\left(1-{\hat{a}}_i{\hat{b}}_i\right)-n_{i1}{\left(1-{\hat{a}}_i\right)}^2}{4n_{i1}{\left(1-{\hat{a}}_i\right)}^2}+\frac{{\hat{\sigma }}_i^4}{2\left(n_{i1}-1\right)},$$where ${\hat{a}}_i={\left(1-{\hat{\delta }}_i\right)}^{n_i-1}$ and ${\hat{b}}_i=1+\left(n_i-1\right){\hat{\delta }}_i$. The ordinary form of the common log-transformed CV is given by

(8) $$\tilde{\phi }=\frac{\sum _{i=1}^k{w}_i{\hat{\phi }}_i}{\sum _{i=1}^k{w}_i},$$where $w_i=1/\hat{V}\left({\hat{\phi }}_i\right)$. Accordingly, the common CV is defined as

(9) $$\tilde{\eta }=\exp \left(\tilde{\phi }\right)=\exp \left(\frac{\sum _{i=1}^k{w}_i{\hat{\phi }}_i}{\sum _{i=1}^k{w}_i}\right).$$

Here, the methods to establish the confidence intervals for the common CV for delta-lognormal distributions are provided in detail.

Mover

Following the method of Zou & Donner (2008), let ${\phi }_1$ and ${\phi }_2$ be the parameter of interest and then let ${\hat{\phi }}_1$ and ${\hat{\phi }}_2$ be the independent estimators of ${\phi }_1$ and ${\phi }_2$, respectively. Furthermore, the lower and upper confidence limits for ${\phi }_1$ + ${\phi }_2$ are

(23) $$C{I}_{{\phi }_1+{\phi }_2}=\left[L_{{\phi }_1+{\phi }_2},U_{{\phi }_1+{\phi }_2}\right]={\hat{\phi }}_1+{\hat{\phi }}_2\pm z_{\alpha /2}\sqrt{\widehat{Var}\left({\hat{\phi }}_1\right)+\widehat{Var}\left({\hat{\phi }}_2\right)},$$

Subsequently, let $l_i$ and $u_i$, for $i=1,2$, be the lower and upper bounds of the confidence interval for ${\phi }_i$, respectively. Since $l_i$ and $u_i$ provide the possible parameter values, then $l_1+l_2$ is close to $L_{{\phi }_1+{\phi }_2}$ and $u_1+u_2$ is close to $U_{{\phi }_1+{\phi }_2}$. To obtain the lower limit $L_{{\phi }_1+{\phi }_2}$, the estimated variance of ${\hat{\phi }}_i$ at ${\phi }_i=l_i$ is given by

(24) $$\widehat{Var}\left({\hat{\phi }}_{l_i}\right)=\frac{{\left(\widehat{{\phi }_i}-l_i\right)}^2}{z_{\alpha /2}^2}.$$

Similarly, to obtain the upper limit $U_{{\phi }_1+{\phi }_2}$, the estimated variance of ${\hat{\phi }}_i$ at ${\phi }_i=u_i$ is given by

(25) $$\widehat{Var}\left({\hat{\phi }}_{u_i}\right)=\frac{{\left(u_i-{\hat{\phi }}_i\right)}^2}{z_{\alpha /2}^2}.$$

Next, by substituting $\widehat{Var}\left({\hat{\phi }}_{l_i}\right)$ and $\widehat{Var}\left({\hat{\phi }}_{u_i}\right)$ into Eq. ( 23), we obtain

(26) $$L_{{\phi }_1+{\phi }_2}={\hat{\phi }}_1+{\hat{\phi }}_2-\sqrt{{\left({\hat{\phi }}_1-l_1\right)}^2+{\left({\hat{\phi }}_2-l_2\right)}^2}$$and

(27) $$U_{{\phi }_1+{\phi }_2}={\hat{\phi }}_1+{\hat{\phi }}_2-\sqrt{{\left(u_1-{\hat{\phi }}_1\right)}^2+{\left(u_2-{\hat{\phi }}_2\right)}^2}.$$

Thereby, the unbiased estimate variance of ${\hat{\phi }}_i$ at ${\phi }_i=l_i$ and ${\phi }_i=u_i$ can be expressed as

(28) $$\widehat{Var}\left({\hat{\phi }}_i\right)=\frac{1}{2}\left[\frac{{\left({\hat{\phi }}_i-l_i\right)}^2}{z_{\alpha /2}^2}+\frac{{\left(u_i-{\hat{\phi }}_i\right)}^2}{z_{\alpha /2}^2}\right],i=1,2.$$

When this concept is extended to $k$ parameters, the lower and upper confidence limits for $\upsilon =\sum _{i=1}^k{\phi }_i$ are given by

(29) $$L_{\upsilon }=\upsilon -\sqrt{{\left({\hat{\phi }}_1-l_1\right)}^2+{\left({\hat{\phi }}_2-l_2\right)}^2+\dots +{\left({\hat{\phi }}_k-l_k\right)}^2}$$and

(30) $$U_{\upsilon }=\upsilon +\sqrt{{\left(u_1-{\hat{\phi }}_1\right)}^2+{\left(u_2-{\hat{\phi }}_2\right)}^2+\dots +{\left(u_k-{\hat{\phi }}_k\right)}^2}.$$

According to Krishnamoorthy & Oral (2017) and recalling the common log-transformed CV from Eq. ( 8), the upper and lower confidence limits for ${\sigma }_i^2$ and ${\delta }_i$ are required to construct the confidence interval for the common CV of delta-lognormal distributions. Since the estimate of ${\sigma }_i^2$ is

(31) $${\hat{\sigma }}_i^2=\frac{1}{n_{i1}-1}\sum _{j=1}^{n_{i1}}{\left[\ln \left(x_{ij}\right)-{\hat{\mu }}_i\right]}^2,$$where $\left(n_{i1}-1\right){\hat{\sigma }}_i^2/{\sigma }_i^2\sim {\chi }_{n_{i1}-1}^2$, the $100\left(1-\alpha \right)\mathrm{\%}$ confidence interval for ${\sigma }_i^2$ is derived as

(32) $$C{I}_{{\sigma }_i^2}=\left(l_{{\sigma }_i^2},u_{{\sigma }_i^2}\right)=\left[\frac{\left(n_{i1}-1\right){\hat{\sigma }}_i^2}{{\chi }_{1-\alpha /2,n_{i1}-1}^2},\frac{\left(n_{i1}-1\right){\hat{\sigma }}_i^2}{{\chi }_{\alpha /2,n_{i1}-1}^2}\right].$$

To construct the confidence interval for ${\delta }_i$, the concept of the variance stabilizing transformation proposed by DasGupta (2008) and Wu & Hsieh (2014) was used. Therefore, the confidence interval for ${\delta }_i$ is given by

(33) $$C{I}_{{\delta }_i}=\left(l_{{\delta }_i},u_{{\delta }_i}\right)={\sin }^2\left(\arcsin \sqrt{{\hat{\delta }}_i}\pm \frac{1}{2\sqrt{n_i}}{Z}_{i\left(1-\alpha /2\right)}\right).$$

Since ${\phi }_i=\left\{\ln \left[\exp \left({\sigma }_i^2\right)-{\delta }_i\right]-\ln \left({\delta }_i\right)\right\}/2$, then let

(34) $$l_i=\frac{1}{2}\left\{\ln \left[\exp \left(l_{{\sigma }_i^2}\right)-l_{{\delta }_i}\right]-\ln \left(l_{{\delta }_i}\right)\right\}$$and

(35) $$u_i=\frac{1}{2}\left\{\ln \left[\exp \left(u_{{\sigma }_i^2}\right)-u_{{\delta }_i}\right]-\ln \left(u_{{\delta }_i}\right)\right\},$$for $i=1,2,\dots ,k$. Therefore, the $100\left(1-\alpha \right)\mathrm{\%}$ confidence interval for $\tilde{\eta }$ based on MOVER can be written as

(36) $$C{I}_{\tilde{\eta }}^m=\left[L_{\tilde{\eta }}^m,U_{\tilde{\eta }}^m\right],$$where

(37) $$L_{\tilde{\eta }}^m=\exp \left(\tilde{\phi }-\sqrt{\sum _{i=1}^k{w}_i^2{\left({\hat{\phi }}_i-l_i\right)}^2/\sum _{i=1}^k{w}_i^2}\right)$$and

(38) $$U_{\tilde{\eta }}^m=\exp \left(\tilde{\phi }+\sqrt{\sum _{i=1}^k{w}_i^2{\left(u_i-{\hat{\phi }}_i\right)}^2/\sum _{i=1}^k{w}_i^2}\right).$$

Results

Monte Carlo simulation studies

The R statistical program was used to run the Monte Carlo simulation study and calculate the results for evaluating the performances of FGCI, MOVER, and the Bayesian intervals with the independent Jeffreys or uniform priors. The criteria for choosing the best performing confidence interval were coverage probability $\ge$ 0.95 and the shortest expected length for each scenario tested. To generate the data, we set the number of populations as $k=3,5,10$; sample sizes as $n_1=n_2=\dots =n_k=n=25,50,100$; probabilities of non-zero values as ${\delta }_1={\delta }_2=\dots ={\delta }_k=\delta =0.2,0.5,0.8$; and variances as ${\sigma }_1^2={\sigma }_2^2=\dots ={\sigma }_k^2={\sigma }^2=0.1,0.5,1.0,2.0$. For each combination of parameters, 10,000 simulation runs were generated together with 2,000 replications for FGCI and the Bayesian approaches by applying Algorithms 1 and 2, respectively.

(For i = 1 to M)

Generate $x_{ij},i=1,2,\dots ,k,j=1,2,\dots ,n_i$ from a delta-lognormal distribution.

Compute ${\hat{\delta }}_i$ and ${\hat{\sigma }}_i^2$.

(For j = 1 to K)

Generate $U_i\sim {\chi }_{n_{i1}-1}^2$, $Beta\left(n_{i1},n_{i0}+1\right)$, and $Beta\left(n_{i1}+1,n_{i0}\right)$.

Compute $R_{{\sigma }_i^2}$, $R_{{\delta }_i}$, $R_{{\hat{\phi }}_i}$, and $R_{\tilde{\eta }}$.

(End j loop)

Compute the 100(1 − α/2) % confidence interval for $\tilde{\eta }$.

(End i loop)

DOI: 10.7717/peerj.12858/table-7

(For i = 1 to M)

Generate $x_{ij},i=1,2,\dots ,k,j=1,2,\dots ,n_i$ from a delta-lognormal distribution.

Compute ${\hat{\delta }}_i$ and ${\hat{\sigma }}_i^2$.

(For j = 1 to K)

Generate the posterior densities of ${\delta }_i^{\ast }\mid x_{ij}$.

1. Independent Jeffreys prior: ${\delta }_i^{\ast }\mid x_{ij}\sim Beta\left(n_{i0}+\frac{1}{2},n_{i1}+\frac{1}{2}\right)$.

2. Uniform prior: ${\delta }_i^{\ast }\mid x_{ij}\sim Beta\left(n_{i0}+1,n_{i1}+1\right)$.

Generate the posterior densities of ${\sigma }_i^2\mid x_{ij}$

1. Independent Jeffreys prior: ${\sigma }_i^2\mid x_{ij}\sim Inv-Gamma\left[\frac{n_{i1}-1}{2},\frac{\left(n_{i1}-1\right){\hat{\sigma }}_i^2}{2}\right]$.

2. Uniform prior: ${\sigma }_i^2\mid x_{ij}\sim Inv-Gamma\left[\frac{n_{i1}-2}{2},\frac{\left(n_{i1}-2\right){\hat{\sigma }}_i^2}{2}\right]$.

Compute ${\hat{\phi }}_i$, $\hat{V}\left({\hat{\phi }}_i\right)$, and $\tilde{\eta }$.

(End j loop)

Compute the 100(1 − α/2) % confidence intervals and credible intervals for $\tilde{\eta }$.

(End i loop)

DOI: 10.7717/peerj.12858/table-8

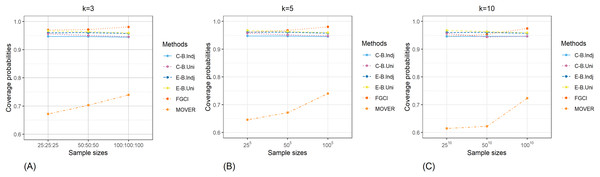
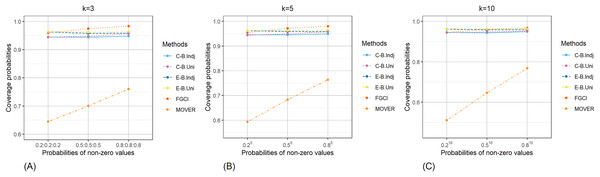
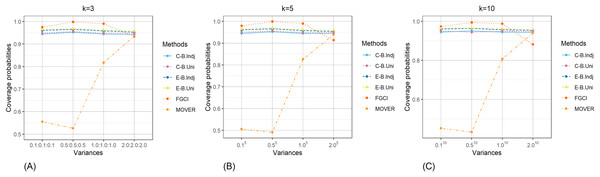
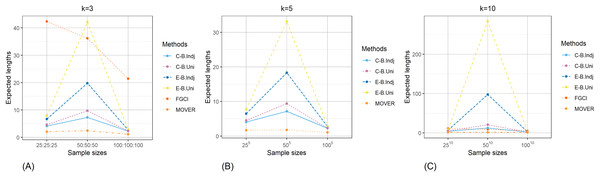
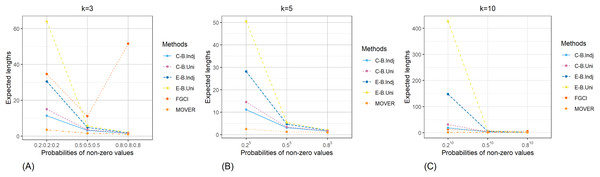
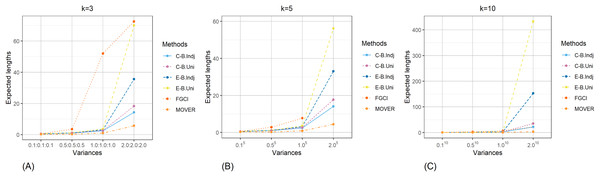
The result for the 95% confidence and credible intervals for the common CV of delta-lognormal distributions for various sample sizes, probabilities of non-zero values, and variances are reported in Tables 1–3 and displayed in Figs. 3–8. The equal-tailed Bayesian credible intervals based on the independent Jeffreys or uniform priors produced coverage probabilities close to or greater than the nominal confidence level for almost all of the scenarios whereas the others could achieve this in only some of them. Furthermore, in terms of the expected lengths, the equal-tailed based on independent Jeffreys prior were shorter than the uniform prior for all cases. In addition, the expected lengths of the Bayesian credible interval based on the independent Jeffreys prior were shorter than the others in almost every case when ${\sigma }_i^2=0.5$. For all $k$ and sample sizes together with ${\sigma }_i^2=1,2$, the expected lengths of the equal-tailed Bayesian based on the independent Jeffreys prior were the shortest when ${\delta }_i=0.2,0.5$, while MOVER had the shortest expected lengths for ${\delta }_i=0.8$. For FGCI, the coverage probabilities and their expected lengths were very wide for all cases in which it is not reasonable for the construction of confidence interval. However, the equal-tailed Bayesian interval based on the independent Jeffreys prior can be used to derive the confidence interval for the common CV of delta-lognormal distributions since it produced coverage probabilities $\ge$ 0.95 for almost all cases, although the expected lengths were not always shorter than the other methods in some cases.

Table 1:

The results for the 95% two-sided confidence intervals for the common CV of delta-lognormal distributions for $k=3$.

ni	δi	${\sigma }_i^2$	Coverage probabilities (Expected lengths)
			FGCI	E-B.Indj	E-B.Uni	C-B.Indj	C-B.Uni	MOVER
25	0.5	0.1	0.9740	0.9537	0.9601	0.9357	0.9411	0.2536
			(0.7272)	(0.7291)	(0.7249)	(0.7079)	(0.7037)	(0.3519)
		0.5	0.9983	0.9689	0.9734	0.9518	0.9564	0.5541
			(4.2363)	(1.5221)	(1.6132)	(1.3548)	(1.4144)	(0.4478)
		1.0	0.9775	0.9613	0.9672	0.9429	0.9518	0.7872
			(28.1984)	(4.2206)	(4.7049)	(3.2428)	(3.5018)	(1.4839)
		2.0	0.9027	0.9528	0.9600	0.9408	0.9485	0.9133
			(7.4009)	(34.3846)	(42.9115)	(18.1504)	(20.8831)	(8.0816)
	0.8	0.1	0.9959	0.9676	0.9823	0.9479	0.9699	0.1611
			(0.5921)	(0.4309)	(0.4381)	(0.4188)	(0.4263)	(0.1540)
		0.5	0.9994	0.9658	0.9700	0.9575	0.9687	0.7894
			(9.1319)	(0.8848)	(0.9205)	(0.8193)	(0.8486)	(0.3732)
		1.0	0.9890	0.9563	0.9623	0.9526	0.9589	0.9445
			(274.3619)	(2.0822)	(2.1950)	(1.7915)	(1.8716)	(1.1456)
		2.0	0.9204	0.9518	0.9567	0.9464	0.9548	0.9705
			(13.9706)	(9.4530)	(10.2449)	(6.8908)	(7.3329)	(4.7949)
50	0.2	0.1	0.9510	0.9611	0.9554	0.9424	0.9346	0.5551
			(1.2188)	(1.3347)	(1.3067)	(1.2849)	(1.2573)	(0.7675)
		0.5	0.9940	0.9734	0.9721	0.9589	0.9580	0.4001
			(5.3666)	(3.0387)	(3.3163)	(2.5773)	(2.7137)	(0.7416)
		1.0	0.9668	0.9663	0.9700	0.9436	0.9473	0.6903
			(61.6887)	(10.2196)	(12.7965)	(6.8382)	(7.7720)	(2.3985)
		2.0	0.8941	0.9573	0.9674	0.9403	0.9473	0.8591
			(10.2166)	(205.9432)	(470.3159)	(61.6888)	(89.7961)	(16.4537)
	0.5	0.1	0.9746	0.9573	0.9592	0.9454	0.9463	0.7691
			(0.4985)	(0.5278)	(0.5246)	(0.5178)	(0.5146)	(0.3383)
		0.5	0.9991	0.9665	0.9689	0.9517	0.9533	0.4400
			(2.3261)	(0.9184)	(0.9322)	(0.8743)	(0.8851)	(0.2156)
		1.0	0.9977	0.9554	0.9608	0.9435	0.9462	0.7862
			(27.7099)	(2.0097)	(2.0670)	(1.8046)	(1.8466)	(0.7810)
		2.0	0.9383	0.9498	0.9545	0.9385	0.9434	0.9348
			(24.2678)	(8.0467)	(8.3999)	(6.4058)	(6.6170)	(3.8741)
	0.8	0.1	0.9960	0.9675	0.9766	0.9514	0.9658	0.3313
			(0.3738)	(0.3069)	(0.3088)	(0.3013)	(0.3033)	(0.1317)
		0.5	0.9997	0.9607	0.9665	0.9507	0.9593	0.7357
			(1.6860)	(0.5521)	(0.5606)	(0.5316)	(0.5397)	(0.2003)
		1.0	0.9980	0.9563	0.9584	0.9458	0.9513	0.9516
			(5.1781)	(1.1695)	(1.1911)	(1.0905)	(1.1088)	(0.7058)
		2.0	0.9464	0.9521	0.9554	0.9483	0.9515	0.9824
			(293.3686)	(3.9878)	(4.0900)	(3.4771)	(3.5501)	(2.7229)
100	0.2	0.1	0.9461	0.9591	0.9537	0.9434	0.9352	0.8726
			(0.8134)	(0.9378)	(0.9241)	(0.9166)	(0.9035)	(0.6757)
		0.5	0.9965	0.9691	0.9679	0.9508	0.9470	0.2665
			(3.4026)	(1.6493)	(1.6684)	(1.5542)	(1.5659)	(0.3647)
		1.0	0.9947	0.9613	0.9631	0.9433	0.9420	0.6284
			(13.0351)	(3.7143)	(3.8315)	(3.2441)	(3.3177)	(1.0735)
		2.0	0.9326	0.9547	0.9601	0.9384	0.9410	0.8846
			(181.1185)	(16.6849)	(17.6932)	(12.4128)	(12.9191)	(6.1118)
100	0.5	0.1	0.9685	0.9578	0.9585	0.9445	0.9462	0.8992
			(0.3491)	(0.3777)	(0.3764)	(0.3724)	(0.3710)	(0.2704)
		0.5	0.9996	0.9604	0.9632	0.9495	0.9501	0.3157
			(1.3697)	(0.6091)	(0.6121)	(0.5933)	(0.5961)	(0.1058)
		1.0	0.9990	0.9553	0.9574	0.9379	0.9415	0.7982
			(3.7435)	(1.2257)	(1.2378)	(1.1620)	(1.1725)	(0.4857)
		2.0	0.9668	0.9545	0.9548	0.9442	0.9475	0.9549
			(32.9162)	(4.0100)	(4.0691)	(3.6039)	(3.6477)	(2.4343)
	0.8	0.1	0.9950	0.9581	0.9676	0.9450	0.9559	0.5995
			(0.2532)	(0.2194)	(0.2200)	(0.2164)	(0.2170)	(0.1167)
		0.5	1.0000	0.9562	0.9595	0.9465	0.9503	0.7093
			(1.0189)	(0.3729)	(0.3754)	(0.3648)	(0.3672)	(0.1204)
		1.0	0.9992	0.9537	0.9562	0.9443	0.9465	0.9560
			(2.3875)	(0.7571)	(0.7631)	(0.7289)	(0.7344)	(0.4796)
		2.0	0.9662	0.9496	0.9522	0.9445	0.9479	0.9872
			(16.9898)	(2.3221)	(2.3448)	(2.1655)	(2.1851)	(1.7740)

DOI: 10.7717/peerj.12858/table-1

Note:

E-B.Indj and E-B.Uni represented the respective equal-tailed Bayesian intervals based on independent Jeffreys and uniform priors, and C-B.Indj and C-B.Uni represented the respective Bayesian credible intervals based on independent Jeffrey’s and uniform priors. Bold indicates the coverage probability ≥ 0.95 and the shortest expected length.

Table 2:

The results for the 95% two-sided confidence intervals for the common CV of delta-lognormal distributions for $k=5$.

ni	δi	${\sigma }_i^2$	Coverage probabilities (Expected lengths)
			FGCI	E-B.Indj	E-B.Uni	C-B.Indj	C-B.Uni	MOVER
25	0.5	0.1	0.9834	0.9596	0.9646	0.9374	0.9438	0.1197
			(0.7505)	(0.7303)	(0.7259)	(0.7088)	(0.7045)	(0.3301)
		0.5	0.9997	0.9710	0.9746	0.9531	0.9595	0.4830
			(3.7038)	(1.5339)	(1.6273)	(1.3637)	(1.4246)	(0.3499)
		1.0	0.9737	0.9600	0.9647	0.9423	0.9506	0.7917
			(8.9088)	(4.2573)	(4.7602)	(3.2717)	(3.5364)	(1.2034)
		2.0	0.8603	0.9541	0.9613	0.9410	0.9483	0.9096
			(1,933.3646)	(32.2422)	(40.4745)	(17.2785)	(19.8882)	(5.9389)
	0.8	0.1	0.9997	0.9697	0.9840	0.9485	0.9730	0.0701
			(0.6148)	(0.4309)	(0.4382)	(0.4187)	(0.4265)	(0.1438)
		0.5	1.0000	0.9639	0.9713	0.9574	0.9671	0.8460
			(3.4724)	(0.8808)	(0.9159)	(0.8160)	(0.8447)	(0.3396)
		1.0	0.9836	0.9583	0.9637	0.9510	0.9614	0.9642
			(10.7410)	(2.0830)	(2.1955)	(1.7916)	(1.8719)	(1.0345)
		2.0	0.8901	0.9517	0.9576	0.9493	0.9560	0.9807
			(3.67E+04)	(9.7354)	(10.5885)	(7.0602)	(7.5199)	(4.1883)
50	0.2	0.1	0.9532	0.9604	0.9526	0.9401	0.9310	0.4326
			(1.2400)	(1.3288)	(1.3007)	(1.2798)	(1.2516)	(0.7301)
		0.5	0.9987	0.9743	0.9730	0.9556	0.9546	0.2693
			(5.1024)	(3.0276)	(3.2924)	(2.5680)	(2.7012)	(0.5583)
		1.0	0.9647	0.9655	0.9690	0.9441	0.9467	0.6413
			(16.6022)	(10.0192)	(12.3389)	(6.7304)	(7.6160)	(1.6963)
		2.0	0.8562	0.9539	0.9636	0.9407	0.9498	0.8377
			(3.08E+05)	(187.9496)	(362.9737)	(60.4077)	(85.9882)	(10.2873)
	0.5	0.1	0.9803	0.9609	0.9630	0.9457	0.9501	0.7854
			(0.5169)	(0.5283)	(0.5251)	(0.5183)	(0.5151)	(0.3322)
		0.5	1.0000	0.9661	0.9688	0.9519	0.9550	0.3610
			(2.4601)	(0.9163)	(0.9303)	(0.8721)	(0.8834)	(0.1694)
		1.0	0.9990	0.9582	0.9620	0.9446	0.9489	0.8114
			(6.0419)	(2.0201)	(2.0770)	(1.8123)	(1.8540)	(0.6894)
		2.0	0.9276	0.9529	0.9570	0.9440	0.9463	0.9459
			(1,419.0445)	(7.9109)	(8.2496)	(6.2988)	(6.5140)	(3.4257)
	0.8	0.1	0.9996	0.9640	0.9743	0.9492	0.9641	0.2056
			(0.3905)	(0.3067)	(0.3087)	(0.3012)	(0.3032)	(0.1238)
		0.5	1.0000	0.9650	0.9703	0.9546	0.9618	0.8014
			(1.8753)	(0.5542)	(0.5624)	(0.5337)	(0.5412)	(0.1868)
		1.0	0.9993	0.9541	0.9547	0.9456	0.9501	0.9760
			(4.2360)	(1.1716)	(1.1949)	(1.0922)	(1.1119)	(0.6724)
		2.0	0.9321	0.9552	0.9576	0.9518	0.9555	0.9932
			(45.8789)	(4.0252)	(4.1253)	(3.5054)	(3.5809)	(2.5923)
100	0.2	0.1	0.9507	0.9586	0.9514	0.9442	0.9368	0.9115
			(0.8347)	(0.9364)	(0.9220)	(0.9150)	(0.9014)	(0.6683)
		0.5	0.9995	0.9667	0.9640	0.9484	0.9459	0.1510
			(3.6099)	(1.6424)	(1.6607)	(1.5490)	(1.5595)	(0.2957)
		1.0	0.9980	0.9626	0.9638	0.9438	0.9443	0.6174
			(8.7078)	(3.7265)	(3.8501)	(3.2539)	(3.3293)	(0.8938)
		2.0	0.9178	0.9578	0.9612	0.9435	0.9464	0.8842
			(1,302.6130)	(16.4958)	(17.4678)	(12.2904)	(12.7883)	(5.0720)
100	0.5	0.1	0.9707	0.9559	0.9573	0.9452	0.9448	0.9455
			(0.3598)	(0.3784)	(0.3768)	(0.3730)	(0.3715)	(0.2692)
		0.5	1.0000	0.9618	0.9621	0.9494	0.9494	0.2473
			(1.5439)	(0.6091)	(0.6120)	(0.5933)	(0.5958)	(0.0838)
		1.0	1.0000	0.9541	0.9577	0.9425	0.9459	0.8244
			(3.9566)	(1.2291)	(1.2421)	(1.1653)	(1.1763)	(0.4456)
		2.0	0.9672	0.9541	0.9558	0.9444	0.9464	0.9717
			(15.8155)	(4.0068)	(4.0614)	(3.6001)	(3.6428)	(2.2992)
	0.8	0.1	0.9985	0.9622	0.9688	0.9499	0.9598	0.5759
			(0.2646)	(0.2194)	(0.2200)	(0.2164)	(0.2171)	(0.1142)
		0.5	1.0000	0.9607	0.9647	0.9483	0.9549	0.7699
			(1.1485)	(0.3738)	(0.3762)	(0.3656)	(0.3679)	(0.1127)
		1.0	1.0000	0.9499	0.9530	0.9430	0.9461	0.9857
			(2.6290)	(0.7549)	(0.7615)	(0.7270)	(0.7329)	(0.4680)
		2.0	0.9598	0.9516	0.9523	0.9466	0.9489	0.9969
			(6.1687)	(2.3383)	(2.3604)	(2.1803)	(2.1988)	(1.7304)

DOI: 10.7717/peerj.12858/table-2

Note:

Bold indicates the coverage probability ≥ 0.95 and the shortest expected length.

Table 3:

The results for the 95% two-sided confidence intervals for the common CV of delta-lognormal distributions for $k=10$.

ni	δi	${\sigma }_i^2$	Coverage probabilities (Expected lengths)
			FGCI	E-B.Indj	E-B.Uni	C-B.Indj	C-B.Uni	MOVER
25	0.5	0.1	0.9750	0.9578	0.9648	0.9353	0.9420	0.0262
			(0.7387)	(0.7284)	(0.7247)	(0.7070)	(0.7032)	(0.3056)
		0.5	0.9999	0.9682	0.9716	0.9500	0.9550	0.3282
			(3.7907)	(1.5242)	(1.6165)	(1.3565)	(1.4164)	(0.2387)
		1.0	0.9721	0.9568	0.9646	0.9396	0.9486	0.7670
			(7.9902)	(4.2284)	(4.7050)	(3.2447)	(3.5022)	(0.9681)
		2.0	0.8170	0.9544	0.9617	0.9399	0.9486	0.9124
			(27.2845)	(35.0401)	(46.9413)	(18.2674)	(21.6147)	(4.5799)
	0.8	0.1	1.0000	0.9695	0.9829	0.9511	0.9734	0.0118
			(0.5753)	(0.4324)	(0.4395)	(0.4201)	(0.4275)	(0.1331)
		0.5	1.0000	0.9658	0.9731	0.9566	0.9677	0.9021
			(3.4758)	(0.8807)	(0.9150)	(0.8155)	(0.8441)	(0.3032)
		1.0	0.9796	0.9538	0.9594	0.9494	0.9584	0.9804
			(7.0148)	(2.0894)	(2.2045)	(1.7966)	(1.8782)	(0.9335)
		2.0	0.8306	0.9552	0.9601	0.9488	0.9557	0.9900
			(37.3845)	(9.6166)	(10.4834)	(6.9970)	(7.4504)	(3.6911)
50	0.2	0.1	0.9490	0.9603	0.9553	0.9430	0.9356	0.2560
			(1.2475)	(1.3345)	(1.3065)	(1.2848)	(1.2569)	(0.6806)
		0.5	0.9979	0.9723	0.9724	0.9541	0.9518	0.1051
			(5.3392)	(3.0554)	(3.3326)	(2.5815)	(2.7157)	(0.3897)
		1.0	0.9650	0.9636	0.9685	0.9442	0.9463	0.5255
			(11.0842)	(10.4725)	(12.9382)	(6.9200)	(7.8607)	(1.1454)
		2.0	0.8124	0.9575	0.9658	0.9442	0.9522	0.8009
			(53.4270)	(1,142.6720)	(3,369.2176)	(122.0329)	(222.4721)	(6.6526)
	0.5	0.1	0.9700	0.9601	0.9632	0.9453	0.9495	0.7897
			(0.5115)	(0.5278)	(0.5248)	(0.5177)	(0.5149)	(0.3240)
		0.5	1.0000	0.9672	0.9702	0.9516	0.9553	0.2112
			(2.6159)	(0.9159)	(0.9302)	(0.8720)	(0.8828)	(0.1163)
		1.0	0.9970	0.9596	0.9621	0.9458	0.9507	0.8171
			(6.1760)	(2.0213)	(2.0769)	(1.8134)	(1.8535)	(0.6006)
		2.0	0.8956	0.9540	0.9584	0.9415	0.9459	0.9652
			(15.6125)	(8.0203)	(8.3825)	(6.3810)	(6.5924)	(3.0276)
	0.8	0.1	0.9976	0.9652	0.9745	0.9507	0.9651	0.0741
			(0.3688)	(0.3067)	(0.3088)	(0.3012)	(0.3033)	(0.1153)
		0.5	0.9596	0.9557	0.9487	0.9433	0.8688	0.9300
			(2.0073)	(0.5524)	(0.5606)	(0.5322)	(0.5395)	(0.1726)
		1.0	0.9975	0.9554	0.9598	0.9451	0.9516	0.9910
			(4.2894)	(1.1691)	(1.1913)	(1.0899)	(1.1089)	(0.6371)
		2.0	0.8936	0.9554	0.9579	0.9513	0.9566	0.9992
			(7.8557)	(4.0458)	(4.1465)	(3.5224)	(3.5975)	(2.4638)
100	0.2	0.1	0.9445	0.9577	0.9534	0.9437	0.9349	0.9551
			(0.8343)	(0.9358)	(0.9215)	(0.9147)	(0.9008)	(0.6605)
		0.5	0.9996	0.9680	0.9669	0.9550	0.9487	0.0384
			(3.8651)	(1.6467)	(1.6645)	(1.5521)	(1.5622)	(0.2242)
		1.0	0.9942	0.9614	0.9623	0.9459	0.9445	0.5322
			(8.9324)	(3.7215)	(3.8417)	(3.2516)	(3.3245)	(0.6967)
		2.0	0.8966	0.9539	0.9579	0.9389	0.9412	0.8751
			(22.0831)	(16.7659)	(17.8464)	(12.4326)	(12.9750)	(4.1159)
100	0.5	0.1	0.9612	0.9547	0.9562	0.9431	0.9439	0.9816
			(0.3580)	(0.3777)	(0.3764)	(0.3724)	(0.3711)	(0.2680)
		0.5	1.0000	0.9623	0.9624	0.9512	0.9519	0.1266
			(1.6621)	(0.6085)	(0.6115)	(0.5927)	(0.5954)	(0.0594)
		1.0	1.0000	0.9561	0.9582	0.9433	0.9462	0.8441
			(4.1570)	(1.2303)	(1.2424)	(1.1663)	(1.1766)	(0.4028)
		2.0	0.9565	0.9497	0.9523	0.9404	0.9409	0.9899
			(8.2323)	(4.0172)	(4.0756)	(3.6098)	(3.6542)	(2.1795)
	0.8	0.1	0.9923	0.9598	0.9679	0.9494	0.9589	0.5202
			(0.2599)	(0.2192)	(0.2198)	(0.2163)	(0.2168)	(0.1112)
		0.5	1.0000	0.9590	0.9631	0.9501	0.9547	0.8216
			(1.2451)	(0.3745)	(0.3770)	(0.3663)	(0.3686)	(0.1055)
		1.0	1.0000	0.9551	0.9568	0.9476	0.9483	0.9975
			(2.7509)	(0.7554)	(0.7609)	(0.7273)	(0.7324)	(0.4582)
		2.0	0.9518	0.9497	0.9526	0.9469	0.9480	0.9999
			(4.0077)	(2.3383)	(2.3610)	(2.1800)	(2.1998)	(1.6955)

DOI: 10.7717/peerj.12858/table-3

Note:

Bold indicates the coverage probability ≥ 0.95 and the shortest expected length.