Modeling ocean distributions and abundances of natural- and hatchery-origin Chinook salmon stocks with integrated genetic and tagging data

Methods overview

We aim to provide the first model to formally integrate information from (1) large-scale, long-term CWT programs and (2) more recently developed monitoring based on GSI sampling of fisheries catches, to derive estimates of marine distribution and abundance for Chinook salmon. We first describe the CWT-based model structure developed in Shelton et al. (2019) and Shelton et al. (2021) before describing the additional GSI-associated components, including incorporation of GSI mixture observations, stock-specific age structure, freshwater run size, and total marine fisheries catches. Several of these components act as model constraints to address challenges in integrating CWT and GSI data sources into a single, joint model.

CWT-based (CWT-only) model structure

We first present the model structure and data of the CWT-based state-space model, described in detail in Shelton et al. (2021), which served as the foundation for subsequently integrating GSI data. In this model, we estimate the spatio-temporal dynamics of tagged releases of Chinook salmon from distinct stocks, using a state-space model that distinguishes biological processes from population observations. We track each CWT release group (i.e., juvenile salmon reared in a hatchery and released together) from initial release abundance (ranging between 9,000 and 3.5 million) through final escapement for spawning. We describe the corresponding age classification schedule in Table S1.1. Patterns in CWT recoveries from fisheries-dependent and fisheries-independent sampling in marine and freshwater environments provide information on four biological processes: (a) the mortality of fish prior to spring of age 2; (b) fishing mortality by age and ocean region among fleets; (c) spatial distributions of stocks among discrete ocean regions; and (d) age-specific departure of fish from the ocean due to maturation and spawning. The model compares model-predicted CWT recoveries to observed recoveries across releases, times, and regions to find parameters that minimize the distance between predictions and observations.

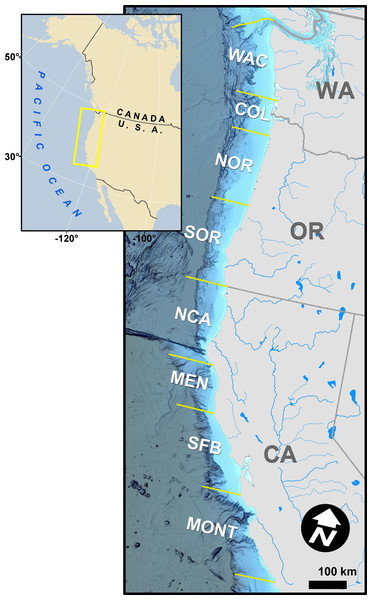
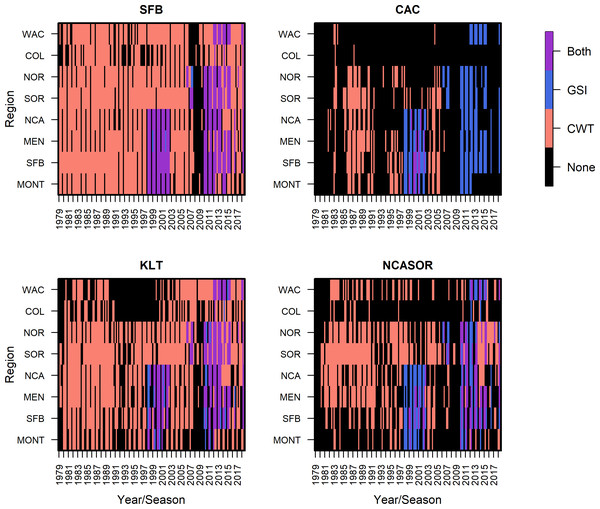
In a departure from previous modeling efforts (Shelton et al., 2019; Shelton et al., 2021), we reduced the number of modeled stocks, releases, and ocean regions to facilitate the subsequent integration of GSI data and focus comparisons across stocks of primary interest. We followed Shelton et al. (2019) in assuming spatial distributions of stocks did not vary annually. We tracked the population dynamics of 284 tagged groups of Chinook salmon from between 1979 and 2018, which resulted in 82,542 observations of CWT catch (Table S2.1). The selected four stocks were fall-run Chinook salmon from California’s Central Valley (code: SFB), coastal rivers and streams south of Klamath River to the Russian River (CAC), Klamath and Trinity Rivers (KLT), and coastal rivers and streams in northern California and southern Oregon, south of the Elk River and north of Klamath River (NCASOR). These stocks reflect finer resolution groupings than those specified in previous analyses and largely map onto the structure of both managed Evolutionarily Significant Units(ESUs) and baseline reporting groups used in GSI (Seeb et al., 2007; Clemento et al., 2014; Shelton et al., 2019; Shelton et al., 2021). We modeled distribution along the U.S. west coast, divided into 8 ocean regions (i.e., Monterey (MONT), San Francisco Bay (SFB), Mendocino (MEN), Northern California (NCA), Southern Oregon (SOR), Northern Oregon (NOR), Columbia River (COL), and Washington (WAC); see Fig. 1) due to limited availability of GSI data north of WAC; we rarely observed CWT recoveries for the four focal stocks north of WAC (Table S2.5; see also Shelton et al., 2019; Shelton et al., 2021). We incorporated three additional years of CWT recovery data compared to previous analyses (2016–2018; Shelton et al., 2021) to maximize overlap between the temporal coverage of CWT and GSI sampling (Fig. 2). Finally, we changed the definition of seasons spring and winter to better match patterns of fishery harvest (Supplemental Information S1). We implemented the statistical model in Stan (Stan Development Team, 2022) as structured in R (rstan v2.21.2; R Core Team, 2023; Stan Development Team, 2023). Full details on model structure and data for this and other portions of the model are provided in Supplemental Information S1.

Integrated CWT- and GSI-based (CWT+GSI) model structure

In addition to tracking the abundance and distribution of focal stocks using hatchery-derived CWT release groups, we separately track the abundance and distribution of total populations from each of the focal stocks (i.e., including hatchery- and natural-origin fish). More specifically, we treated and tracked all fish “released” (i.e., out-migrated) into the marine environment in a given year and from a given stock as a single total release group. Tracking total release groups is necessary for us to link model processes to GSI data because GSI provides information on the composition of all fish, not just tagged fish. These new estimates also expand our inference to provide insights into the abundance of a given stock at a given time and place. We only track these total release groups starting at the spring of age 2 (i.e., after any juvenile mortality occurs following initial entry into the ocean), as we lack sufficient data on total out-migrating smolt abundances. Estimation of life history processes for the total release groups is based in part on GSI data to inform relative stock composition in marine fisheries. Integrating GSI data into the model simultaneously estimates shared life history parameters for CWT and total release groups and provides estimates of spatial distribution and abundance reflective of fish both with and without CWTs.

We incorporated individual assignment data from dockside GSI sampling of recreational landings from California in 1998–2002 and GSI sampling of commercial catch from California, Oregon, and Washington in 2006-2014 into the model to inform the abundance and distribution of total release groups; GSI sampling from commercial fisheries relied on voluntary participation and data collection by fishermen (Satterthwaite et al., 2014; Bellinger et al., 2015; Satterthwaite et al., 2015; Fig. 2; Supplemental Information S2). Our use of individual assignment probabilities, rather than raw genotype data, to generate GSI observations was intended to reduce computation requirements and facilitate use of publicly available GSI datasets; however, we emphasize that we used all individual probability-of-group-membership data for each sampled fish, and not just maximum assignment probability, to generate unbiased estimates of stock composition (Koljonen, Pella & Masuda, 2005). In total, we included GSI data spanning 139 unique region-season combinations for two fisheries (i.e., commercial troll, recreational), including a total of 63,018 Chinook salmon sampled for GSI. We selected these datasets based on their spatial and temporal coverage and available sample sizes for characterizing fishery composition. Relative availability of GSI and CWT data varies among stocks; for stocks with more extensive CWT tagging efforts like SFB, CWT observations greatly outnumber GSI observations, while there were similar numbers of CWT and GSI observations for rarer and less supplemented stocks like CAC (Fig. 2).

Similar to our treatment of CWT data, we compared predicted patterns of stock-specific fishery catch to observed stock compositions from GSI sampling. However, in contrast to CWT observations that provide information on the specific age of recovered fish, GSI data only provide information on relative contributions of stocks to the mixture of sampled fish (e.g., approximately 12 of 200 sampled fish in a given region, season, and year are assigned to stock SFB). Furthermore, GSI data can include genetic assignments for stocks other than the four focal stocks (i.e., non-focal stocks like Columbia River Chinook salmon stocks); these can contribute substantially to GSI sampling in ocean regions progressively further north. Our model structure accounts for these complexities. We also note that the GSI reporting group for SFB includes Feather River spring-run fish along with late-fall fish and the KLT reporting group includes both Klamath River fall- and spring-run fish, due to limitations in the available GSI baselines (Seeb et al., 2007; Clemento et al., 2014). Therefore, to an extent, GSI information will reflect information on more than strictly fall-run fish for these two stocks. However, fall-run is numerically dominant for both stocks (Pacific Fishery Management Council, 2020).

To incorporate GSI mixture observations in our model structure, we compare the expected proportional contributions of each focal stock to fisheries harvest to observed GSI data using a zero-and-one inflated Dirichlet regression model with estimated overdispersion (Jensen et al., 2022). This model structure allows for zero and non-integer GSI observations of focal stocks—that is, instances in which none or all the observed fish derive from a given stock—in addition to an overdispersion term that implicitly allows the model to weight the importance of GSI data relative to competing data sources, including CWT data (i.e., greater overdispersion, as measured by a smaller overdispersion parameter, indicates reduced model weighting of GSI data).

To calculate expected proportional contributions of each focal stock to harvest, we first obtain expected catches for a given stock r, region l, season s, year c, and gear g (μ_1,l,s,c,r,g) by summing expected catches across total release groups representing all available ages. Release group-specific expected catches already are estimated in the model as a function of group abundance, spatial distribution, and fishery mortality rate. We use the total number of GSI sampled fish and summed number of fish assigned to focal stocks F using GSI to estimate the expected proportion of sampled catch comprised of focal stocks (p_2,l,s,c,F,g), then estimate the total expected catch across all stocks μ_1,l,s,c,g by dividing the expected catch summed across all focal stocks (μ_1,l,s,c,F,g) by this expected proportion (μ_1,l,s,c,g = μ_1,l,s,c,F,g/p_2,l,s,c,F,g). This expansion is necessary to account for the fact that we only model catches for four focal stocks but total fisheries catch often includes additional stocks. Finally, we estimate the expected proportional contribution of each focal stock r to total harvest by dividing expected stock-specific catch μ_1,l,s,c,r,g by μ_1,l,s,c,g.

Because the complete model struggled to converge, we implemented several additional model constraints. In the absence of release abundance data for total release groups (e.g., number of out-migrating smolts in a given year), we constrained estimates of total release abundances to biologically feasible values using the following data: (1) annual estimates of stock-specific run size (i.e., the number of mature adults that enter freshwater to spawn) when available, (2) estimates of total fishery landings by season, region, and fishery type, and (3) within-model estimates of CWT release group abundances. First, using total release groups within the model, we obtained the expected number of fish entering freshwater across all ages for each stock in a given stock and year; we then minimized the distance between these numbers and independent estimates of run size generated from assorted survey data using a lognormal likelihood with fixed standard deviation values (Supplemental Information S2). Second, we compared total expected catch for recreational and commercial fisheries for all seasons and regions from 1998–2014 (i.e., μ_1,l,s,c,g) to corresponding independent estimates of landings using a normal likelihood and a fixed coefficient of variation (Pacific Fishery Management Council, 2019). To deal with seasons, regions, and years without the corresponding GSI data necessary to estimate total expected catch (i.e., no data to estimate the proportion of focal stocks in expected catch, p_2,l,s,c,F,g), we estimated these proportions hierarchically using a logit-normal likelihood, expected mean proportions of focal stocks in each region, and an estimated standard deviation. The hierarchical structure facilitates borrowing of information from seasons, regions, and years with the necessary GSI data to directly estimate p_2,l,s,c,F,g. Third, to further constrain estimates of abundance and improve model convergence, we specify the abundance of total release groups as the sum of the expected number of CWT-tagged fish (i.e., already estimated internally in the model and informed by known CWT release sizes and CWT fisheries recoveries) and the modeled number of non-CWT-tagged fish (i.e., including both untagged hatchery- and natural-origin fish); this functionally establishes the CWT abundance as the lower bound of total abundance and reduces the occurrence of unrealistically low abundance estimates for some release groups. Finally, the model allows process variability in estimates of CWT and total release group abundances: we constrained the process variability to be identical for every release (i.e., either CWT or total) associated with the same stock and brood year, based on the implicit assumption that effects of population drivers not included in our model are shared by releases from the same stock and brood year.

Exploration of synthetic age structure (CWT+GSI+Age)

Based on persistent challenges in achieving model convergence for estimates of total release group abundances for the CWT+GSI model (see Results), we added an exploratory set of age-structure constraints to the model by providing synthetic samples of ages. Specifically, for a given season, year, and stock, we provide counts of aged fish, generated from the product of fixed age proportions (i.e., either ages 2–5 or 3–5, depending on season) and a specified number of sampled fish, as part of a new multinomial likelihood below. ${\displaystyle A_{.,s,c,r}\sim Multinomial\left(p_{3,.,s,c,r}\right).}$

Specifically, counts of aged fish for each season s, year c, and stock r, or A_.,s,c,r, are used as a form of prior to constrain the proportional contributions of each release age to the total stock abundance, or p_3,.,s,c,r. We provide artificial counts of aged fish due to a lack of systematic data collection of age structure for catches in the marine environment. We estimated fixed age proportions using reconstructed total Klamath River Fall Chinook ocean abundances (Pacific Fishery Management Council, 2021) that we assumed applied to CAC and NCASOR as well; we provide separate proportions for SFB based on both expectations of skew to younger ages and expert judgment (Carvalho et al., 2023). We recognize these proportions are coarse, imprecise values, and are primarily intended to demonstrate the value of improved data availability in the future. Furthermore, although the inclusion of CWT data in the KLT cohort reconstruction, alongside our use of CWT recoveries in this model framework, could represent double-weighting of these data to some extent, we note that a large fraction of age data for the reconstruction was obtained from unmarked fish. We anticipated this synthetic age structure would constrain model flexibility in estimating abundances of total release groups and subsequently improve model convergence.

Model analyses

We first ran the model with only CWT-based catch observations (CWT-only) using the previously described number of stocks, release groups, regions, and years of data, and we characterized estimates of seasonal ocean distribution for each stock. We then ran the model with both CWT- and GSI-based catch observations, but no synthetic age structure (CWT+GSI), and characterized both estimates of seasonal ocean distributions and total abundances for each stock. Finally, we ran the model with CWT- and GSI-based catch observations, in addition to synthetic age structure (CWT+GSI+Age), and characterized improvements in model convergence in addition to any changes in estimates of seasonal ocean distribution and abundance.

We ran each model with six chains, 400 burn-in iterations, and 1,400 retained iterations. We primarily characterized model convergence using R-hat (Gelman & Rubin, 1992; Vehtari et al., 2020).

Statement on data availability

Raw and processed data, including CWT and GSI catch observations, estimates of run size, and estimates of landings, in addition to the corresponding processing scripts, are available at Zenodo (DOI 10.5281/zenodo.8057794) or by contacting the authors.

GSI observations

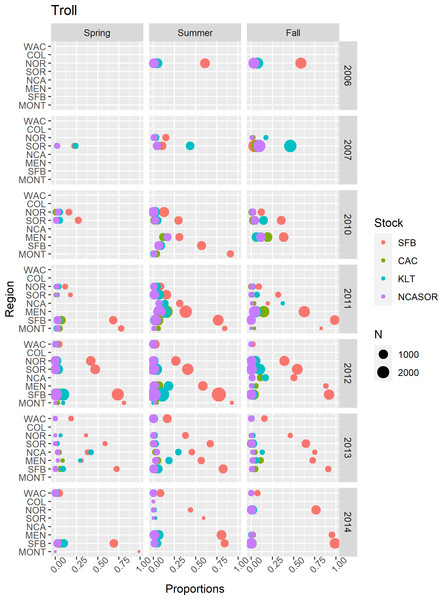
In the CWT+GSI and CWT+GSI+Age models, we included GSI observations from every region, years 1998–2002, 2006–2007, and 2009–2014, and spring, summer, and fall seasons across both commercial troll and recreational hook-and-line fisheries (Supplemental Information S2). Lack of consistent fishing effort in winter resulted in a lack of winter-based GSI data, and observations from the more northern regions COL and WAC were relatively rare. For the GSI observations from the commercial troll fishery (Fig. 3), the SFB stock generally predominated observed catch, particularly in southern spatial regions. In some seasons and years, the KLT stock contributed the most to sampled catch among focal stocks; this generally occurred in either the NCA or SOR regions. The total contribution of the four focal stocks to sampled catch generally decreased with increasing latitude, consistent with their spawning locations. We present GSI observations from the recreational fishery in Fig. S2.12; these observations were restricted to California regions, years 1998–2002, and were again predominated by the SFB stock.

CWT-based (CWT-only) model

We observed satisfactory model convergence for the CWT-only model ($\hat{R}<1.01$ for all parameters). Detailed model diagnostics for this and subsequent models are shared in Supplemental Information S3.

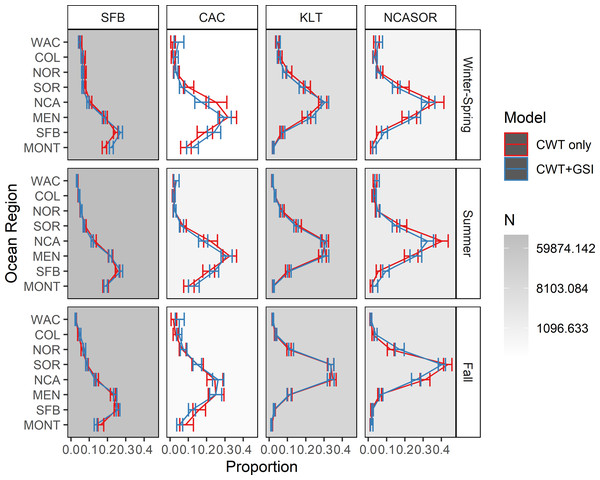
We present estimates of seasonal spatial distribution for the four focal stocks, including 95% credible intervals, in Fig. 4. The estimated spatial distributions of SFB correspond well to those estimated in Shelton et al. (2019) and Shelton et al. (2021), as expected, but also to other qualitative estimates of ocean distribution (e.g., Weitkamp, 2010; Satterthwaite et al., 2013; Bellinger et al., 2015; Satterthwaite et al., 2015). This stock generally occurs between approximately Morro Bay (CA) and Cape Falcon (OR), and is particularly concentrated in the MONT, SFB, and MEN regions. The spatial distribution estimated for CAC is the most comprehensive one for this stock to date, based on spatial extent and the amount of utilized data, and exhibits a more northerly distribution than SFB, predominantly occurring in the MEN and NCA regions. Estimated distributions for KLT are concentrated more northerly still, with the greatest proportion of the stock generally occurring in the NCA region. Finally, the NCASOR stock had the most northerly distribution, with the greatest proportion of the stock occurring in the NCA and SOR regions; the estimated distribution also is the most comprehensive to date for this stock. Estimates of spatial distribution for CAC and NCASOR have wider credible intervals than those estimated for SFB and KLT, consistent with the lower data availability for these stocks. There were minor but inconsistent differences in seasonal distributions for each stock, further supporting the inclusion of seasonality in the model structure.

CWT- and GSI-based (CWT+GSI) model

The CWT+GSI model exhibited some challenges in model convergence (median $\hat{R}=1.01$, $\hat{R}<1.01$ and $\hat{R}<1.1$ for 48% and 88% of tracked parameters). Most issues in model convergence were associated with new estimates of abundance for total release groups (Table S3.1). In particular, the initial abundance at model age 1, before application of fishing or natural mortality, were not fully estimable; there are many combinations of abundances for individual cohorts that can produce abundances similar to the GSI observations (see Supplemental Information S3 and below for more details and discussion).

Estimated ocean distributions for the CWT-only and CWT+GSI models were generally similar, with increasingly northerly distributions for stocks with more northerly spawning distributions (Fig. 4). However, ocean distributions differed between models for some stocks and seasons. For SFB, the CWT+GSI model estimated a more southerly distribution in winter-spring and lower occurrence in MONT in fall, based on non-overlapping 95% credible intervals, relative to the CWT-only model; all other estimated distributions had overlapping intervals. Similarly, although all credible intervals overlapped for CAC, the CWT+GSI model indicated a more southerly distribution in winter-spring and summer and a more northerly distribution in fall. Estimated spatial distributions were highly similar among models for KLT, as all credible intervals again overlapped. For NCASOR, the CWT+GSI model indicated ocean distributions were generally more diffuse but did not show any consistent shifts to either the north or south. Credible intervals for NCASOR did not overlap between models for several regions in both summer and fall. The width of credible intervals did not differ appreciably between the CWT-only and CWT+GSI models.

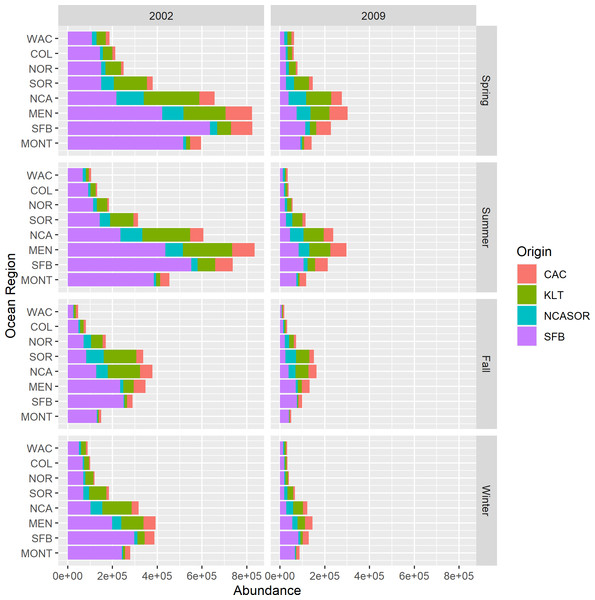
New parameter estimates from the CWT+GSI model include total estimates of stock abundance over time. Because we estimated abundances of total release groups over time, we also were able to calculate estimates of total stock abundance over time for years 1998–2014 (i.e., abundances of all tracked ages). We present example estimates of regional and seasonal stock abundances for 2002 and 2009 (Fig. 5). These years represented convenient example years with very different estimates of stock contributions and total abundance to illustrate the value of these new parameter estimates. Estimated stock abundances in 2002 were high, exceeding 800,000 fish across focal stocks for some regions in spring and summer, and were dominated by the SFB stock. In 2009, estimated stock abundances were noticeably lower and more heterogeneous across stocks. Relative distributions of total fish abundance among regions also varied by year as a function of proportional stock abundances; fish were distributed more northerly overall when northern origin stocks like KLT were predominant. Although not shown, we also can present estimates of uncertainty in stock abundances via 95% credible intervals as part of standard model output. These estimates represent novel historical estimates of relative and total abundances for an assemblage of both rare and abundant Chinook salmon stocks, with the obvious caveat that the model struggled to converge in estimating these values.

The CWT+GSI model also generated some model parameter estimates that differed noticeably from those estimated by the CWT-only model. Specifically, the CWT+GSI model estimated higher juvenile mortality rates and fishery mortality rates than CWT-only, with subsequent effects on estimates of CWT and total release group abundances over time (Supplemental Information S3). This shift in estimated mortality rates shows instability in estimation of these mortality terms as we add data and model complexity, and suggests that further investigation may be required to identify which set of mortality rates is most defensible.

Synthetic age structure (CWT+GSI+Age) model

We added synthetic age structure to the CWT+GSI model in an attempt to improve model convergence, particularly for estimates of total release group abundances over time. The CWT+GSI+Age model still exhibited challenges in overall model convergence (median $\hat{R}=1.01$, $\hat{R}<1.01$ and $\hat{R}<1.1$ for 49% and 90% of tracked parameters). Addition of age structure-related model constraints did improve convergence for estimates of abundance for total release groups, as well as other parameters, but estimates of initial abundance at model age 1 before application of fishing or natural mortality again failed to converge (Table S3.2). The fact that the synthetic age structure did not resolve all issues in model convergence is unsurprising, based on our specification of fixed age proportions from a KLT-based cohort reconstruction. Failure to improve convergence for initial total release group abundances indicates additional data or model constraints still are required to resolve these parameter estimates.

Estimates of ocean distribution for focal stocks did not differ appreciably between the CWT+GSI and CWT+GSI+Age models, suggesting that difficulty in model convergence for some GSI-based parameters did not substantially affect estimates of spatial distribution for models that include GSI-based components (Fig. S3.26). Additionally, estimates of total stock abundances by region, season, and year also did not differ substantially (Fig. S3.27). The only parameter we observed to change with the inclusion of synthetic data was the overdispersion term for GSI, which indicated less weight is applied to GSI data for the CWT+GSI+Age model.