Enhanced trajectory tracking for quadrotors: disturbance observer state feedback control

Quadcopter dynamics

In quadrotor control, the body frame allows for the definition of the total thrust and rotational torques asthe total thrust T and rotational torques in the body frame can be defined as (1)${\displaystyle {\mathrm{T}}_{\mathrm{total}}=\sum _{i=1}^4{T}_i=b_t\sum _{i=1}^4{\omega }_i^2,{\tau }_{\varphi }=d_{mm}{b}_t\left({\omega }_4^2-{\omega }_2^2\right),{\tau }_{\theta }=d_{mm}{b}_t\left({\omega }_3^2-{\omega }_1^2\right),{\tau }_{\psi }=k_d\left({\omega }_1^2+{\omega }_3^2-{\omega }_2^2-{\omega }_4^2\right),}$ where k_d is the drag constant, ω_i is the angular speed of the i_th rotor, d_mm denotes the distance extending from the rotor to the center of mass of the quadcopter, b_t represents the thrust constant, which is dependent on variables including air density, as well as the dimensions of the quadcopter propeller, specifically its length and radius.

The rotor torque τ_Motori around its axis of rotation is opposite to the aerodynamic drag, which leads to (2)${\displaystyle {\tau }_{M_i}=b{\omega }_i^2+I_M{\dot{\omega }}_i,}$ where b is also the drag constant and I_M is the inertia moment associated with the quadcopter’s rotor. The $\dot{\omega }$ can be neglected under quasi-static state, so that (3)${\displaystyle {\tau }_{M_i}=b{\omega }_i^2.}$

For each rotor, the rotation axis also moves in the fixed frame of the fuselage, thus generating the gyroscopic torque (4)${\displaystyle {\tau }_{gyro}=\sum _{i=1}^4{I}_M\left(\Omega \times U_z\right){\omega }_i,}$ where U_z is the unit vector along inertial z-axis and Ω is the angular velocity.

When transitioning from the quadcopter’s body coordinate system to the inertial coordinate system, a rotation matrix is employed below, ${\displaystyle {\mathrm{R}}_{\mathrm{o}}=\left[\begin{array}{ccc}\hfill C_{\theta }{C}_{\psi }\hfill & \hfill S_{\theta }{S}_{\varphi }{C}_{\psi }-C_{\varphi }{S}_{\psi }\hfill & \hfill S_{\theta }{C}_{\psi }{C}_{\varphi }+S_{\varphi }{S}_{\psi }\hfill \\ \hfill C_{\theta }{S}_{\psi }\hfill & \hfill S_{\theta }{S}_{\varphi }{S}_{\psi }+C_{\varphi }{C}_{\psi }\hfill & \hfill S_{\theta }{S}_{\psi }{S}_{\varphi }-S_{\varphi }{C}_{\psi }\hfill \\ \hfill -S_{\theta }\hfill & \hfill S_{\varphi }{C}_{\theta }\hfill & \hfill C_{\varphi }{C}_{\theta }\hfill \end{array}\right],}$ where S_x = sin(x) and C_x = cos(x), with x = θ or ψ. In addition, from the angular velocities $\dot{\eta }={\left[\dot{\varphi },\dot{\theta },\dot{\psi }\right]}^T$ of inertial frame to the rates of angular motion Ω, where Ω = [p, q, r]^T, we have (5)${\displaystyle \Omega =\mathit{F}\dot{\eta },}$ where the transformation matrix is (6)${\displaystyle \mathit{F}=\left[\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill -sin\theta \hfill \\ \hfill 0\hfill & \hfill cos\varphi \hfill & \hfill sin\varphi cos\theta \hfill \\ \hfill 0\hfill & \hfill -sin\varphi \hfill & \hfill cos\varphi cos\theta \hfill \end{array}\right].}$

For the translational dynamics of the quadcopter establishing. According to Newton’s second law, (7)${\displaystyle m\left[\begin{array}{c}\hfill \ddot{x}\hfill \\ \hfill \ddot{y}\hfill \\ \hfill \ddot{z}\hfill \end{array}\right]=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill -mg\hfill \end{array}\right]+{\mathrm{R}}_{\mathrm{o}}\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill {\mathrm{T}}_{\mathrm{total}}\hfill \end{array}\right].}$

Expending the equation, we have (8)${\displaystyle \ddot{x}=-\frac{k_x}{m}\dot{x}+\frac{{\mathrm{T}}_{\mathrm{total}}}{m}\left(sin\theta cos\psi cos\varphi +sin\varphi sin\psi \right),\ddot{y}=-\frac{k_y}{m}\dot{y}+\frac{{\mathrm{T}}_{\mathrm{total}}}{m}\left(sin\theta sin\psi cos\varphi -sin\varphi cos\psi \right),\ddot{z}=-\frac{k_z}{m}\dot{z}+\frac{{\mathrm{T}}_{\mathrm{total}}}{m}cos\varphi cos\theta -g,}$ where $\ddot{x}$, $\ddot{y}$, and $\ddot{z}$ represent the acceleration in their respective axes. kx, ky and kz denote the coefficients of air friction, while $\dot{x},\dot{y},and\dot{z}$ are the velocities in the x −, y −, and z − axes, respectively.

In accordance with Euler’s equation of motion, the rotational dynamics of quadcopter is ${\displaystyle \left[\begin{array}{c}\hfill \dot{p}\hfill \\ \hfill \dot{q}\hfill \\ \hfill \dot{r}\hfill \end{array}\right]=\left[\begin{array}{ccc}\hfill 1/I_x\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1/I_y\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1/I_z\hfill \end{array}\right]\left[\begin{array}{c}\hfill {\tau }_{\varphi }\hfill \\ \hfill {\tau }_{\theta }\hfill \\ \hfill {\tau }_{\psi }\hfill \end{array}\right]+\left[\begin{array}{c}qr\left(I_y-I_z\right)/I_x\hfill \\ pr\left(I_z-I_x\right)/I_y\hfill \\ pq\left(I_x-I_y\right)/I_z\hfill \end{array}\right].}$

Simplify the above equation, which leads to (9)${\displaystyle \dot{p}=\frac{{\tau }_{\varphi }}{I_x}+\frac{rq\left(I_y-I_z\right)}{I_x},\dot{q}=\frac{{\tau }_{\theta }}{I_y}+\frac{rp\left(I_z-I_x\right)}{I_y},\dot{r}=\frac{{\tau }_{\psi }}{I_z}+\frac{qp\left(I_x-I_y\right)}{I_z},}$ where $\dot{p}$, $\dot{q}$, and $\dot{r}$ stand for the angular acceleration parameters within the quadcopter body-centric coordinate system. I_x, I_y and I_z represent the inertia tensors associated with the x −, y −, and z − axes, respectively.

Moreover, the relationship between the Euler angular velocities $\dot{\varphi }$, $\dot{\theta },\dot{\psi }$ and the angular velocities (p, q, r) is expressed as follows (10)${\displaystyle \left[\begin{array}{c}\hfill \dot{\varphi }\hfill \\ \hfill \dot{\theta }\hfill \\ \hfill \dot{\psi }\hfill \end{array}\right]=\left[\begin{array}{ccc}\hfill 1\hfill & \hfill T_{\theta }{S}_{\varphi }\hfill & \hfill T_{\theta }{C}_{\varphi }\hfill \\ \hfill 0\hfill & \hfill C_{\varphi }\hfill & \hfill -S_{\varphi }\hfill \\ \hfill 0\hfill & \hfill \frac{S_{\varphi }}{C_{\theta }}\hfill & \hfill \frac{C_{\varphi }}{C_{\theta }}\hfill \end{array}\right]\left[\begin{array}{c}p\hfill \\ q\hfill \\ r\hfill \end{array}\right].}$

Expending the equation, we have (11)${\displaystyle \dot{\varphi }=p+q{T}_{\theta }{S}_{\varphi }+r{T}_{\theta }{C}_{\varphi },\dot{\theta }=q{C}_{\varphi }-r{S}_{\varphi },\dot{\psi }=q\frac{S_{\varphi }}{C_{\theta }}+r\frac{C_{\varphi }}{C_{\theta }},}$ where T_x = tan(x), S_x = sin(x), and C_x = cos(x), with x = ϕ or θ; $\dot{\varphi },\dot{\theta }$, and $\dot{\psi }$ are the angular velocities within the inertial coordinate system along the x −, y −, and z − axes, respectively.

State space model

Define $\dot{x}=a$, $\dot{y}=b$ and $\dot{z}=c$, the state space model contains 12 state variables for the highly coupled quadcopter system: ${\displaystyle \dot{x}=a,\dot{y}=b,\dot{z}=c,\dot{a}=-\frac{k_x}{m}a+\frac{{\mathrm{T}}_{\mathrm{total}}}{m}\left(sin\theta cos\psi cos\varphi +sin\varphi sin\psi \right),\dot{b}=-\frac{k_y}{m}b+\frac{{\mathrm{T}}_{\mathrm{total}}}{m}\left(sin\theta sin\psi cos\varphi -sin\varphi cos\psi \right),\dot{c}=-\frac{k_z}{m}c+\frac{{\mathrm{T}}_{\mathrm{total}}}{m}cos\varphi cos\theta -g,\dot{p}=\frac{{\tau }_{\varphi }}{I_x}+\frac{rq\left(I_y-I_z\right)}{I_x},\dot{q}=\frac{{\tau }_{\theta }}{I_y}+\frac{rp\left(I_z-I_x\right)}{I_y},\dot{r}=\frac{{\tau }_{\psi }}{I_z}+\frac{qp\left(I_x-I_y\right)}{I_z},\dot{\varphi }=p+q{T}_{\theta }{S}_{\varphi }+r{T}_{\theta }{C}_{\varphi },\dot{\theta }=q{C}_{\varphi }-r{S}_{\varphi },\dot{\psi }=q\frac{S_{\varphi }}{C_{\theta }}+r\frac{C_{\varphi }}{C_{\theta }}.}$

From the above equations, we have ${\displaystyle \dot{X}=f\left(X,U\right),}$ where X = (x, y, z, a, b, c, p, q, r, ϕ, θ, ψ)^T represents the state vertor, $U=\left({\mathrm{T}}_{\mathrm{total}},{\tau }_{\varphi },{\tau }_{\theta },{\tau }_{\psi }\right)$ denotes the thrust vector acting as control input, and Y = (x, y, z, θ) is the output vector. To ensure precise trajectory tracking, the initial focus lies on confirming the alignment of the first three vectors concerning position control. Given the interconnected nature of the quadcopter, an additional check involves validating an angular velocity along the y −axis. This acts as an indirect measure to ascertain the accuracy of the quadcopter’s interlinked system.

Quadcopter input disturbance observer design

Initially, it presupposes an input disturbance denoted as ν(i) in the system, which subsequently results in a transformation of the state-space model. (12)${\displaystyle x_n\left(i+1\right)=A_n{x}_n\left(i\right)+B_n\left(u\left(i\right)+\nu \left(i\right)\right),y\left(i\right)=C_n{x}_n\left(i\right),}$ where u(i) and ν(i) stand for the control inputs, y(i) represents the system responses, and x_n(i) represents the state variable set.

The input disturbance ν(i) is conceptualized as (13)${\displaystyle \nu \left(i\right)=\frac{j^{-1}ϵ\left(i\right)}{D\left(j^{-1}\right)},}$ where ϵ(i) is consistent with the dimension of vector ν(i).

Let the disturbance model D(j⁻¹) be (14)${\displaystyle D\left(j^{-1}\right)=1+d_1{j}^{-1}+d_2{j}^{-2}+d_3{j}^{-3}+\dots +d_{\gamma }{j}^{-\gamma }.}$

Next, use the form of difference equation to express the disturbance vector ν(i + 1): (15)${\displaystyle \nu \left(i+1\right)=-d_1\nu \left(i\right)-d_2\nu \left(i-1\right)-\dots -d_{\gamma }\nu \left(i-\gamma +1\right)+ϵ\left(i\right),}$ where ϵ(i) represents white noise with a mean value of zero.

Following our previous study (Wang & Guan, 2022), by introducing matrix h(i) of size nγ × 1 to represent the disturbance group and presenting it with a state space mode, we have (16)${\displaystyle h\left(i\right)={\left[\begin{array}{cccc}{\nu }^T\left(i\right)\hfill & {\nu }^T\left(i-1\right)\hfill & \cdots \hfill & {\nu }^T\left(i-\gamma +1\right)\hfill \end{array}\right]}^T.}$

Then, using the state space model below to obtain the disturbance (17)${\displaystyle h\left(i+1\right)=A_{dis}h\left(i\right)+B_{ϵ}ϵ\left(i\right),\nu \left(i\right)=C_{ϵ}h\left(i\right).}$

For matrix A_dis, it shows the form as below: ${\displaystyle A_{dis}=\left[\begin{array}{ccccc}\hfill -d_{1}I\hfill & \hfill -d_{2}I\hfill & \hfill \dots \hfill & \hfill -d_{\gamma -1}I\hfill & \hfill -d_{\gamma }I\hfill \\ \hfill I\hfill & \hfill O\hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill O\hfill \\ \hfill O\hfill & \hfill I\hfill & \hfill O\hfill & \hfill \dots \hfill & \hfill ⋮\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill O\hfill & \hfill \dots \hfill & \hfill O\hfill & \hfill I\hfill & \hfill O\hfill \end{array}\right],}$ where B_ϵ is a nγ × n matrix and C_ϵ is a n × nγ matrix, they both have the n × n identity matrix and the rest vertical and horizontal elements of the matrix are zeros. The leftover rows and columns in both matrices consist of zero matrices. O is a n × n zero matrix and I is the identity matrices with same dimensions.

For the disturbance $D\left(j^{-1}\right)$, we have (18)${\displaystyle det\left(j^{-1}I-A_d\right)=D{\left(j^{-1}\right)}^n,}$ where D(j⁻¹) is the disturbance model in backward shift form. Matrix A_dis includes n groups of eigenvalues which related to the zeros of the D(j⁻¹).

The incorporation of the disturbance vector ν(i) into the state space model serves to mitigate the impact of external interference on the state estimate matrix x_n(i). The introduced augmented state matrix is ${\displaystyle x\left(i\right)={\left[\begin{array}{cc}{x}_n^T\left(i\right)\hfill & h{\left(i\right)}^T\hfill \end{array}\right]}^T.}$

We rewrite the previous state space model as ${\displaystyle x_n\left(i+1\right)=A_n{x}_n\left(i\right)+B_n{C}_{ϵ}h\left(i\right)+B_{n}u\left(i\right).}$

Under this condition, an augmented system space model is derived: ${\displaystyle \left[\begin{array}{c}\hfill x_n\left(i+1\right)\hfill \\ \hfill h\left(i+1\right)\hfill \end{array}\right]=\stackrel{\mathcal{A}}{\overbrace{\left[\begin{array}{c}\hfill A_n{B}_n{C}_{ϵ}\hfill \\ \hfill O_1{A}_{dis}\hfill \end{array}\right]}}\left[\begin{array}{c}\hfill x_n\left(i\right)\hfill \\ \hfill h\left(i\right)\hfill \end{array}\right]+\stackrel{B}{\overbrace{\left[\begin{array}{c}\hfill B_n\hfill \\ \hfill O_2\hfill \end{array}\right]}}u\left(i\right)+\left[\begin{array}{c}{O}_3\hfill \\ B_{ϵ}\hfill \end{array}\right]ϵ\left(i\right),}$ where O_1,2,3 are zero matrices to adapt to corresponding dimensions; the integrated A and B matrices are regarded as the augmented matrices of the system.

The output is computed as ${\displaystyle y\left(i\right)=\stackrel{C}{\overbrace{\left[\begin{array}{c}{C}_n{O}_4\hfill \end{array}\right]}}\left[\begin{array}{c}\hfill x_n\left(i\right)\hfill \\ \hfill h\left(i\right)\hfill \end{array}\right],}$ where C is the augmented output matrix, and O₄ is a zero matrix like O_1,2,3.

After establishing the augmented model, we will design the observer on this basis, A and C matrices will be used in the design of this step. First define an observer gain K_ob, it is a matrix with the same dimension as A and C. To get the value of K_ob, we use the discrete-time LQR algorithm. The selected observer gain is to stabilize the state matrix $\left(A-K_{ob}C\right)$ in the closed-loop observer error system deviation dynamics. As a result, the augmented state matrix x(i) becomes amenable to estimation. (19)${\displaystyle \hat{x}\left(i+1\right)=A\hat{x}\left(i\right)+Bu\left(i\right)+K_{ob}\left(y\left(i\right)-C\hat{x}\left(i\right)\right).}$

Noting that in order to ensure that A and C are observable, it is first necessary to ensure that the An and Cn matrices are observable, and the system has no zeroes which related to D(j⁻¹). Under this condition, the observer can operate effectively.

Disturbance observer-based discrete-time state feedback control

Before appling augmented system state representation, converting continuous model to discrete model. The state space model in continuous time can be formulated as follows: (20)${\displaystyle {\dot{x}}_n\left(k\right)=A_c{x}_n\left(k\right)+B_{c}u\left(k\right),}$ (21)${\displaystyle y\left(k\right)=C_c{x}_n\left(k\right).}$

The discrete-time formulation of the state space model can be succinctly articulated as follows: (22)${\displaystyle x_n\left(i+1\right)=A_n{x}_n\left(i\right)+B_{n}u\left(i\right),}$ (23)${\displaystyle y\left(i\right)=C_n{x}_n\left(i\right).}$

Based on the design of adding disturbance to the input and its compensation in the state estimation, the design of the state feedback control is undertaken through the subsequent stepwise procedure. It continues to adopt the state-space formulation detailed in the preceding section, following the design of model: ${\displaystyle x_n\left(i+1\right)=A_n{x}_n\left(i\right)+B_n\left(u\left(i\right)+\nu \left(i\right)\right),y\left(i\right)=C_n{x}_n\left(i\right).}$

Noting that the input vectors are u(i) and ν(i). It assumes that the observational properties are satisfied for matrices An and Cn and that the controllability conditions are met for the pair (A_n, B_n). Moreover, the system avoid the zeros which related to the disturbance occurring at the D(j⁻¹).

We define the intermediary control signal at this stage: ${\displaystyle \tilde{u}\left(k\right)=u\left(k\right)+\mu \left(k\right).}$

Then the original x_n(i + 1) becomes (24)${\displaystyle x_n\left(i+1\right)=A_n{x}_n\left(i\right)+B_n\tilde{u}\left(i\right).}$

Following our previous study (Wang & Guan, 2022), the principle behind state feedback control using a disturbance observer involves designing the state feedback controller K specifically for the intermediate control signal $\tilde{u}\left(k\right)$. This controller aims to handle the estimated variable to effectively compensate for the input disturbance ν(k).

It integrates (x_n(i + 1), h(i + 1)) and y(i) as a complete augmented model ${\displaystyle \left[\begin{array}{c}\hfill x_n\left(i+1\right)\hfill \\ \hfill h\left(i+1\right)\hfill \end{array}\right]=\stackrel{A}{\overbrace{\left[\begin{array}{c}\hfill A_n{B}_n{C}_{ϵ}\hfill \\ \hfill O_1{A}_{dis}\hfill \end{array}\right]}}\left[\begin{array}{c}\hfill x_n\left(i\right)\hfill \\ \hfill h\left(i\right)\hfill \end{array}\right]+\stackrel{B}{\overbrace{\left[\begin{array}{c}\hfill B_n\hfill \\ \hfill O_2\hfill \end{array}\right]}}u\left(i\right)+\left[\begin{array}{c}\hfill O_3\hfill \\ \hfill B_{ϵ}\hfill \end{array}\right]ϵ\left(i\right)y\left(i\right)=\stackrel{C}{\overbrace{\left[\begin{array}{c}{C}_n{O}_4\hfill \end{array}\right]}}\left[\begin{array}{c}\hfill x_n\left(i\right)\hfill \\ \hfill h\left(i\right)\hfill \end{array}\right].}$

Based on this model, we can use the disturbance compensation strategy to get ${\hat{x}}_n\left(i\right)$ and $\hat{\nu }\left(i\right)$ from previous disturbance observer design section.

Deriving the controller K utilizing matrices A_n and B_n to ensure the stability of the closed-loop control system matrix A_n − B_nK, the interim control variable $\tilde{u}\left(i\right)$ is computed as (25)${\displaystyle \tilde{u}\left(i\right)=-K{\hat{x}}_n\left(i\right).}$

Secondly, get the observer gain K_ob using matrices A and C allowing for the estimation of both the input disturbance ν(i) and the state variable x_n(k) within the augmented state space model, resulting in $\hat{\nu }\left(i\right)$ and ${\hat{x}}_n\left(i\right)$.

After that, deducting $\hat{\nu }\left(i\right)$ from $\tilde{u}\left(i\right)$ results in the control variable u(i): (26)${\displaystyle u\left(i\right)=\tilde{u}\left(i\right)-\hat{\nu }\left(i\right).}$

Compare a fixed signal r(i) with our output signal, considering the reference signal r(i), where the observer formulation takes the following form ${\displaystyle \hat{x}\left(i+1\right)=A\hat{x}\left(i\right)+Bu\left(i\right)+K_{ob}\left(y\left(i\right)-r\left(i\right)-C\hat{x}\left(i\right)\right).}$

The (A, B, C) matrices are augmented matrices which contains the input disturbance compensation. Furthermore, it is imperative to validate that the entirety of the eigenvalues pertaining to the observer error system matrix A − K_obC remains strictly bounded within the confines of the unit circle, thereby guaranteeing system stability and observability.

Determined the closed-loop eigenvalue of the state feedback control system based on disturbance observer to ensure the stability of the system. For both x_n(i) and $\hat{p}\left(i\right)$, we adopt the observation error system ${\displaystyle \left[\begin{array}{c}\hfill E_{xp}\left\{{\tilde{x}}_n\left(i+1\right)\right\}\hfill \\ \hfill E_{xp}\left\{\tilde{h}\left(i+1\right)\right\}\hfill \end{array}\right]=\left(A-K_{ob}C\right)\left[\begin{array}{c}\hfill E_{xp}\left\{{\tilde{x}}_n\left(i\right)\right\}\hfill \\ \hfill E_{xp}\left\{\tilde{h}\left(i\right)\right\}\hfill \end{array}\right],}$ where E_xp represents the error variables x_n(i) and $\hat{h}\left(i\right)$, with their expectations denoted as respective values.

In addition, the proposed disturbance observer state feedback control strategy is compared to the traditional Proportional-Integral-Derivative (PID) control strategy based on important performance indicators, including trajectory tracking accuracy, response time, resilience to external disturbances, and algorithm complexity. At first, the proposed technique demonstrates superior precision in accurately following a desired path compared to the classic PID control, especially when dealing with external disturbances. Furthermore, it demonstrates greater proficiency in maneuvering intricate and ever-changing surroundings. In terms of response time, this technique efficiently adjusts control parameters to accommodate variations in external variables, surpassing the performance of conventional PID control. Our system, which includes the use of a disturbance observer, is highly effective in resisting external disturbances. It is particularly adept at withstanding environmental changes like strong winds, ensuring excellent flight stability and trajectory accuracy. This sets it apart from conventional methods. Furthermore, although the complexity of our method’s control algorithm exceeds that of PID control, its benefits in terms of other performance metrics justify this complexity.

Trajectory types

First of all, we have assumed three cases for the reference trajectory in 3D space. The first case is a single straight-line trajectory. The second case is the cylindrical spiral track, which contains sine and cosine curves and can represent the turning or hovering situation of the UAV in general. The third case is the second conic trajectory, which can be understood as a high-order extension in the second case. Because the conic curve contains elliptical, parabolic, and hyperbolic trajectories, it can represent more realistic UAV flight trajectories and has certain representativeness in the aviation field. The simulation results are presented below.

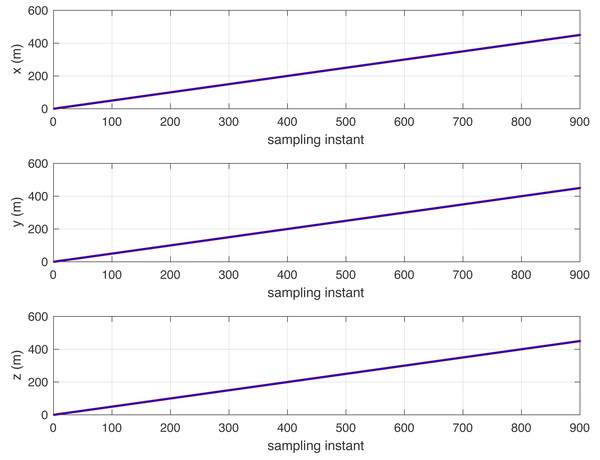
Reference following. Figure 1 shows the reference tracking performance with the integrator mode controller and random walk disturbances: D(j⁻¹) = 1 − j⁻¹.

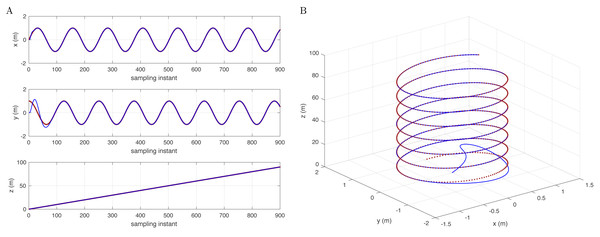
Figure 2 illustrates the simulation results with a sinusoidal mode controller and the disturbance in the corresponding sinusoidal mode: D(j⁻¹) = 1 − 2cos ω_dj⁻¹ + j⁻².

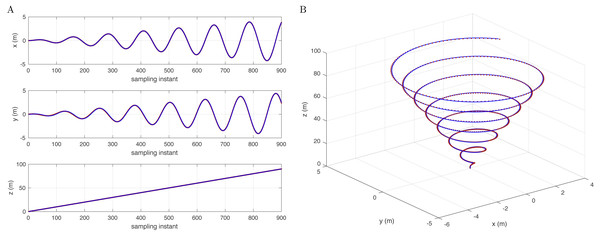
Figure 3A shows that the reference signal is extended to a conic track with a variable turning radius. In addition, Fig. 3B shows an intuitive 3D space simulation result. Figure 1 to Fig. 3 show that for different reference trajectories and controllers, selecting appropriate corresponding disturbance models D(j⁻¹) can complete the disturbance compensation issue and make the simulation results consistent with the reference trajectories.

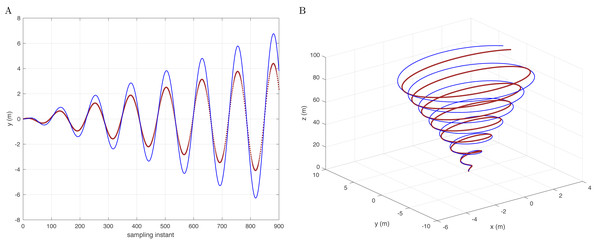
To experiment with a contrast test on the premise of conic trajectory, if the D(j⁻¹) model is changed to not correspond to the controller, the quadcopter will not be able to effectively complete the compensation of disturbance and trajectory tracking. The simulation results are shown in Fig. 4, taking the y −axis as an example.

Unmanned aerial vehicles may undergo alterations in their mass and moment of inertia during actual use, which can be caused by factors such as cargo variations, battery usage, or ambient conditions. Therefore, it is essential to evaluate the stability and efficiency of the control strategy in light of these variations in parameters. This study thoroughly examines the resilience of the suggested control approach when faced with different aircraft parameter fluctuations.

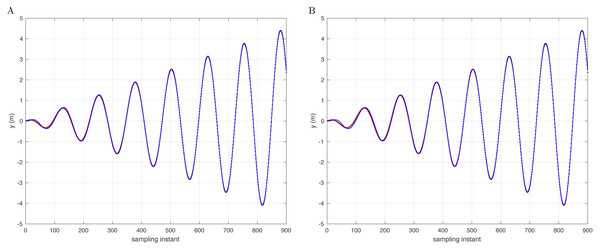
The analysis considers the fluctuation in the weight of the unmanned aerial vehicle, utilizing simulated scenarios that incorporate a gradual rise in weight up to 1.5 kg. Our simulation results show that the suggested control method maintains a high level of trajectory tracking performance even when there are changes in mass that affect how the system moves. This validates the efficacy of the technique in addressing fluctuations in mass. The study examines the impact of changes in the weight of the unmanned aerial vehicle, specifically focusing on cases where the weight decreases. Following a 30% decrease in mass, the trajectory tracking, as illustrated in Fig. 5A, continues to provide very good performance. The simulation effectively retains its tracking performance, similar to its performance before the drop in mass, using the y-axis as an illustration. It ultimately approaches the reference trajectory after approximately two sinusoidal oscillation cycles. The results of the simulation show that the suggested control method consistently achieves a high level of trajectory tracking performance, even when there are changes in mass that affect how the system moves.

Furthermore, a thorough examination of the influence of changes in the moment of inertia on the control system is conducted. After a specific decrease of 15% in inertia, the trajectory tracking, as seen in Fig. 5B, exhibits a comparable pattern. Illustrating the y-axis as an instance, at a small scale, the simulation presently reaches a state of convergence with the reference trajectory after around three cycles of sinusoidal oscillation. At a large scale, the general ability to accurately follow a desired path continues to be exceptional, as the error values consistently stay within the range of 0.002 m.