Dynamic prediction of carbon prices based on the multi-frequency combined model

Feature selection

Feature selection becomes a critical tool when dealing with large, high-dimensional datasets. It helps identify the key features that most significantly influence prediction outcomes, effectively reducing redundancy in the model and enhancing predictive accuracy (Hao & Tian, 2020). Additionally, feature selection contributes to improving the interpretability of the model, providing a more solid foundation and support for data analysis and decision-making. This study employs the partial autocorrelation function (PACF) to determine the optimal historical carbon price data and utilizes the Lasso regression (LASSO) method to select the most relevant external influencing factors.

Cheetah optimization algorithm

COA is a new type of group intelligence optimization algorithm, which is proposed by Amin et al. (2022) in 2022 as a new type of group intelligence optimization algorithm inspired by cheetah hunting in nature, which achieves the position updating by simulating the three strategies of cheetahs’ searching, sitting and waiting, and attacking in the process of hunting, and it has the strong ability of searching for the optimal, and the quick speed of convergence and other characteristics.

Research indicates that cheetahs typically succeed in capturing their prey within 30 s, earning them the title of the “fastest land animal.” In 2022, Amin et al. (2022) introduced a nature-inspired meta-heuristic algorithm for large-scale optimization problems known as the COA. This algorithm simulates the hunting mechanism of cheetahs, with its mathematical model encompassing three strategies: search, wait, and attack.

COA-XGBoost model

XGBoost is a boosting-type model developed by Chen & Guestrin (2016) in 2016, which combines linear solvers with learning algorithms for classification and regression trees. The fundamental idea of this model is to combine multiple decision tree models with lower predictive accuracy using a specific strategy to create a more accurate ensemble model. During the model training process, XGBoost iteratively optimizes the model through gradient boosting, generating a new decision tree in each iteration to fit the residuals produced in the previous iteration. Through this iterative optimization approach, XGBoost can continuously enhance the model’s predictive accuracy and generalization capability. The traditional gradient boosting decision tree (GBDT) method only utilizes the first derivative, while XGBoost performs a second-order Taylor expansion of the loss function, incorporating a regularization term to control model complexity and mitigate overfitting. Additionally, XGBoost employs a more refined evaluation method at the split nodes, enabling it to better capture the nonlinear relationships between features. In recent years, the XGBoost model has demonstrated strong performance in various fields, including financial risk control, healthcare, and natural language processing. The mathematical principles of this model are as follows:

Define the ensemble model of trees as follows:

(7) $${\hat{\mathrm{y}}}_{\mathrm{i}}=\sum _{\mathrm{m}=1}^{\mathrm{M}}{\mathrm{f}}_{\mathrm{m}}\left({\mathrm{x}}_{\mathrm{i}}\right),{\mathrm{f}}_{\mathrm{m}}\in \mathrm{F}.$$

In the equation, ${\hat{y}}_i$ represents the predicted value; $\mathrm{M}$ is the number of decision trees; $\mathrm{F}$ denotes the space of tree selections; and $x_i$ is the $\mathrm{i}$-th input feature.

The loss function of the XGBoost model is given by:

(8) $$\mathrm{L}=\sum _{\mathrm{i}=1}^{\mathrm{n}}\mathrm{l}\left({\mathrm{y}}_{\mathrm{i}},{\hat{\mathrm{y}}}_{\mathrm{i}}\right)+\sum _{\mathrm{m}=1}^{\mathrm{M}}\mathrm{\theta }\left({\mathrm{f}}_{\mathrm{m}}\right).$$

In this equation, the first part of the function represents the prediction error between the XGBoost model’s predicted values and the actual training values, while the second part reflects the complexity of the trees. The main purpose of this second part is to serve as regularization to control the model’s complexity:

(9) $$\mathrm{\theta }\left({\mathrm{f}}_{\mathrm{m}}\right)=\mathrm{\gamma }\mathrm{T}+{\displaystyle \frac{1}{2}\mathrm{\tau }\parallel \mathrm{\omega }{\parallel }^2.}$$

In the equation, $\gamma$ and $\tau$ are penalty factors. During the process of minimizing the loss function, incorporating the incremental function $f_t\left(x_i\right)$ in Eq. (9) can minimize the value of the loss function to the greatest extent. Thus, the objective function for the $\mathrm{t}$-th iteration is given by:

(10) $${\mathrm{L}}^{\left(\mathrm{t}\right)}=\sum _{\mathrm{i}=1}^{\mathrm{n}}\mathrm{l}\left({\mathrm{y}}_{\mathrm{i}},{\hat{\mathrm{y}}}_{\mathrm{i}}\right)+\sum _{\mathrm{m}=1}^{\mathrm{M}}\mathrm{\theta }\left({\mathrm{f}}_{\mathrm{m}}\right)=\sum _{\mathrm{i}=1}^{\mathrm{n}}\mathrm{l}\left({\mathrm{y}}_{\mathrm{i}},{\hat{\mathrm{y}}}_{\mathrm{i}}^{\mathrm{t}-1}+{\mathrm{f}}_{\mathrm{t}}\left({\mathrm{x}}_{\mathrm{i}}\right)\right)+\mathrm{\theta }\left({\mathrm{f}}_{\mathrm{t}}\right).$$

At this point, a second-order Taylor expansion of Eq. (11) is performed to approximate the objective function, and the sample set in each leaf of the $\mathrm{j}$-th tree is defined as $I_j=\{i|q\left(x_i=j\right)\}$. The approximation can be represented as follows:

(11) $$\begin{array}{rl}{\mathrm{L}}^{\left(\mathrm{t}\right)}& \cong \sum _{\mathrm{i}=1}^{\mathrm{n}}\left[{\mathrm{g}}_{\mathrm{i}}{\mathrm{f}}_{\mathrm{t}}\left({\mathrm{x}}_{\mathrm{i}}\right)+\frac{1}{2}{\mathrm{h}}_{\mathrm{i}}{\mathrm{f}}_{\mathrm{t}}^2\left({\mathrm{x}}_{\mathrm{i}}\right)\right]+\mathrm{\theta }\left({\mathrm{f}}_{\mathrm{t}}\right)\cong \sum _{\mathrm{i}=1}^{\mathrm{n}}\left[{\mathrm{g}}_{\mathrm{i}}{\mathrm{f}}_{\mathrm{t}}\left({\mathrm{x}}_{\mathrm{i}}\right)+1/2{\mathrm{h}}_{\mathrm{i}}{\mathrm{f}}_{\mathrm{t}}^2\left({\mathrm{x}}_{\mathrm{i}}\right)\right]+\mathrm{\gamma }\mathrm{T}+\frac{1}{2}\mathrm{\tau }{\mathrm{\omega }}^2\\ & \cong \sum _{\mathrm{j}=1}^{\mathrm{T}}\left[\left(\sum _{\mathrm{i}\in {\mathrm{I}}_{\mathrm{j}}}{\mathrm{g}}_{\mathrm{i}}\right){\mathrm{\omega }}_{\mathrm{j}}+\frac{1}{2}\left(\sum _{\mathrm{i}\in {\mathrm{I}}_{\mathrm{j}}}{\mathrm{h}}_{\mathrm{i}}+\tau \right){\mathrm{\omega }}_{\mathrm{j}}^2\right]+\mathrm{\gamma }\mathrm{T}.\end{array}$$

In this equation, ${\mathrm{g}}_{\mathrm{i}}={\mathrm{\partial }}_{{\hat{\mathrm{y}}}_{\mathrm{i}}^{\mathrm{t}-1}}\mathrm{l}\left({\mathrm{y}}_{\mathrm{i}},{\hat{\mathrm{y}}}_{\mathrm{i}}^{\mathrm{t}-1}\right)$ represents the first derivative of the loss function, and $h_i={\mathrm{\partial }}_{{\hat{y}}_i^{t-1}}^{2}l\left(y_i,{\hat{y}}_i^{t-1}\right)$ denotes the second derivative of the loss function. Defining $G_i=\sum _{i\in I_j}{g}_i$ and ${\mathrm{H}}_{\mathrm{i}}=\sum _{\mathrm{i}\in {\mathrm{I}}_{\mathrm{j}}}{\mathrm{h}}_{\mathrm{i}}$, the following is obtained:

(12) $${\mathrm{L}}^{\mathrm{t}}\cong \sum _{\mathrm{j}=1}^{\mathrm{T}}\left[{\mathrm{G}}_{\mathrm{j}}{\mathrm{\omega }}_{\mathrm{j}}+{\displaystyle \frac{1}{2}\left({\mathrm{H}}_{\mathrm{j}}+\mathrm{\tau }\right){\mathrm{\omega }}_{\mathrm{j}}^2}\right]+\mathrm{\gamma }\mathrm{T}.$$

Taking the partial derivative with respect to $\omega$, the following is obtained:

(13) $${\mathrm{\omega }}_{\mathrm{j}}=-{\displaystyle \frac{{\mathrm{G}}_{\mathrm{j}}}{{\mathrm{H}}_{\mathrm{j}}+\mathrm{\tau }}.}$$

Substituting the weights into the objective function, the following is obtained:

(14) $${\mathrm{L}}^{\left(\mathrm{t}\right)}\cong -{\displaystyle \frac{1}{2}\sum _{\mathrm{j}=1}^{\mathrm{T}}{\displaystyle \frac{{\mathrm{G}}_{\mathrm{j}}^2}{{\mathrm{H}}_{\mathrm{j}}+\mathrm{\tau }}+\mathrm{\gamma }\mathrm{T}}}$$

In the training process of the XGBoost model, the choice of different parameters can significantly impact the prediction results; thus, the model’s performance is largely determined by the selection of parameters. There are a total of 23 hyperparameters in the XGBoost algorithm, which are primarily divided into general parameters for controlling the overall function, booster parameters for managing the details of the booster and learning objective parameters that control the training objectives. The COA-XGBoost combined model uses the five hyperparameters that most significantly affect performance in XGBoost (namely, learning_rate, subsample, colsample_bytree, max_depth, and alpha) as the position vector $\alpha$ of the cheetah in the COA algorithm. Through iterative updates via the COA algorithm, these parameters are continuously optimized until the global optimal position is output as the final parameters for the XGBoost model.

CEEMDAN model

The CEEMDAN algorithm, proposed by Torres et al. (2011) in 2011, is a data-driven algorithm used for signal processing and analyzing nonlinear and adaptive signals. The basic idea is that the original signal is decomposed into a series of IMF and the algorithm parameters are adjusted using adaptive noise, which improves the quality and stability of the decomposition. Compared to the traditional EMD algorithm, the decomposition steps of CEEMDAN are more stable and can reduce randomness in the decomposition process by integrating the results of multiple decompositions. In contrast to the ensemble empirical mode decomposition (EEMD) algorithm, CEEMDAN adds adaptive white noise at each stage, overcoming the significant reconstruction error associated with the EEMD method. CEEMDAN performs exceptionally well in handling complex signals and reducing data fluctuations, making it suitable for addressing the issue of carbon trading price prediction.

The steps of the CEEMDAN decomposition can be summarized as follows:

Step 1: Add an adaptive Gaussian white noise sequence $\sigma n_i\left(t\right)$ to the original sequence $y\left(t\right)$ to obtain a new sequence ${\overline{y}}_i\left(t\right)$ with noise:

(15) $$\begin{array}{c}{\overline{\mathrm{y}}}_{\mathrm{i}}\left(\mathrm{t}\right)=y\left(\mathrm{t}\right)+\sigma {\mathrm{n}}_{\mathrm{i}}\left(\mathrm{t}\right),i=1,2,\cdots \mathrm{N}\end{array}$$where $n_i\left(t\right)$ represents the added white noise, and the intensity of the noise sequence is determined by parameter $\mathrm{\sigma }$.

Step 2: Perform a complete EMD on the noisy original signal to obtain a set of IMFs and a residual component:

(16) $$\begin{array}{c}\mathrm{i}\mathrm{m}{\mathrm{f}}_1\left(\mathrm{t}\right)={\displaystyle \frac{1}{\mathrm{N}}\sum _{\mathrm{i}=1}^{\mathrm{N}}\mathrm{i}\mathrm{m}{\mathrm{f}}_{1\mathrm{i}}\left(\mathrm{t}\right)}\end{array}.$$

At this point, the calculation formula for the residual component $R_1\left(t\right)$ is:

(17) $$\begin{array}{c}{\mathrm{R}}_1\left(\mathrm{t}\right)={\overline{\mathrm{y}}}_{\mathrm{i}}\left(\mathrm{t}\right)-{\mathrm{i}\mathrm{m}\mathrm{f}}_1^{\prime }\left(\mathrm{t}\right)\end{array}.$$

Step 3: The residual is taken as the new input data, and the adaptive white noise sequence $\sigma n_i\left(t\right)$ is added to $R_1\left(t\right)$ to obtain new input data $R_1\left(t\right)+\sigma E_1\left(n_i\left(t\right)\right)$. Here, $E_j(\cdot )$ is the $j$-th intrinsic mode function obtained after EMD decomposition. At this point, the new sequence undergoes EMD decomposition and averaging to obtain the second mode component and the residual component:

(18) $$\mathrm{i}\mathrm{m}{\mathrm{f}}_2\left(\mathrm{t}\right)={\displaystyle \frac{1}{\mathrm{N}}\sum _{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{E}}_1({\mathrm{R}}_1\left(\mathrm{t}\right)+{\mathrm{\sigma }}_1{\mathrm{E}}_1\left({\mathrm{n}}_{\mathrm{i}}\left(\mathrm{t}\right)\right))}$$

(19) $$\begin{array}{c}{\mathrm{R}}_2\left(\mathrm{t}\right)={\mathrm{R}}_1\left(\mathrm{t}\right)-{\mathrm{i}\mathrm{m}\mathrm{f}}_2^{\prime }\left(\mathrm{t}\right)\end{array}$$

Step 4: Repeat Steps 1, 2, and 3 to ultimately obtain the $\mathrm{j}+1$-th mode component and the $\mathrm{j}$-th residual component:

(20) $$\mathrm{i}\mathrm{m}{\mathrm{f}}_{\mathrm{j}+1}\left(\mathrm{t}\right)={\displaystyle \frac{1}{\mathrm{N}}\sum _{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{E}}_1({\mathrm{R}}_{\mathrm{j}}\left(\mathrm{t}\right)+{\mathrm{\sigma }}_{\mathrm{j}}{\mathrm{E}}_{\mathrm{j}}\left({\mathrm{n}}_{\mathrm{i}}\left(\mathrm{t}\right)\right))}$$

(21) $${\mathrm{R}}_{\mathrm{j}}\left(\mathrm{t}\right)={\mathrm{R}}_{\mathrm{j}-1}\left(\mathrm{t}\right)-{\mathrm{i}\mathrm{m}\mathrm{f}}_{\mathrm{j}}^{\prime }\left(\mathrm{t}\right)$$

Step 5: The above steps are repeated until the residual component can no longer be subjected to the EMD decomposition. Finally, the original sequence will be resolved into several intrinsic mode functions and a trend component.

(22) $$\mathrm{y}\left(\mathrm{t}\right)=\sum \mathrm{i}\mathrm{m}\mathrm{f}\left(\mathrm{t}\right)+{\mathrm{R}}_{\mathrm{e}\mathrm{s}}\left(\mathrm{t}\right).$$

After the CEEMDAN has completed the decomposition of the original sequence, appropriate predictive models are applied to each intrinsic mode function component for individual predictions, and the results of each component are aggregated to obtain the final residual prediction results.

COA-XGBoost-CEEMDAN model

This study aims to improve the prediction accuracy of carbon trading prices by proposing a hybrid algorithm based on CEEMDAN, COA, and XGBoost. The main steps of the experiment are as follows:

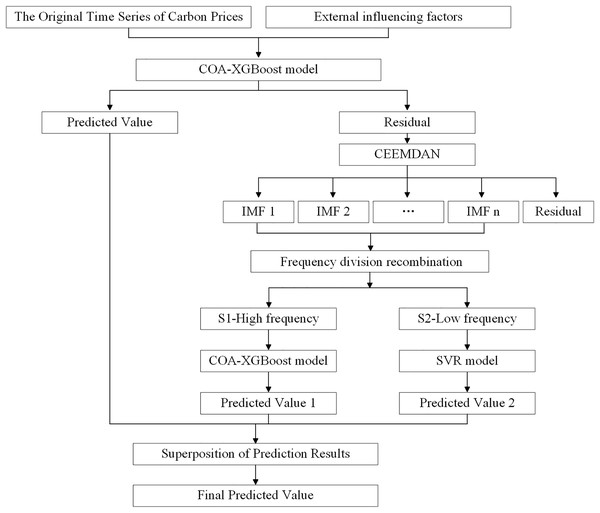
First, the COA algorithm is used to optimize the parameters in the XGBoost model, and the optimized model is used for the initial forecast. Next, CEEMDAN is used to decompose the residual carbon price series, which helps to understand the characteristics and variation patterns of the signal. The decomposed IMFs are then split into high-frequency and low-frequency components, with the COA-XGBoost model and the SVR model used to predict the different frequency components, respectively. Finally, the predicted values of the different mode components are summed with the initial predicted values to obtain the final prediction results of the model. The flowchart is shown in Fig. 1.

In the entire prediction process, COA-XGBoost is used for predictions at two different stages. The considerations for its application at each stage are as follows: first, in the first stage, complex and high-dimensional datasets need to be processed, which puts higher requirements on the robustness and computational efficiency of the model. Based on this, the COA-optimized XGBoost algorithm is selected as the prediction model for the first stage due to its strong fitting ability to high-dimensional nonlinear data. Second, the prediction task in the second stage is relatively straightforward, as the residual sequence obtained from the decomposition of the original data has effectively removed noise and irregular fluctuations, providing a more solid and precise data foundation for subsequent predictions. At this stage, these residuals can be further differentiated into high-and low-frequency components, and the most suitable prediction model can be selected for different frequency data. Since the high-frequency residuals still contain rich and valuable information, and to maintain the overall coherence of the research, this article uses the COA-XGBoost method to handle the prediction of the high-frequency part.

Establishment of primary indicator system

Carbon market and its trading prices

The carbon emissions trading market is a market that combines total control with market trading, characterized by a clear policy orientation. It aims to promote emissions reduction through economic incentive mechanisms, helping to achieve greenhouse gas reduction targets. Governments or regulatory agencies set an overall emissions cap and allocate this cap to various emitting units. These units can meet their emissions requirements through voluntary reductions, purchasing carbon credits, or engaging in carbon offsets. After years of practice and development, the total transaction volume of the eight pilot markets in China has generally shown a steady growth trend, except for a decline in 2020 due to the pandemic. Under the guidance of the “dual carbon” goals, these markets have gradually formed trading mechanisms that align with their development characteristics. In terms of quota setting and allocation, a gradually decreasing control coefficient has been introduced, and efforts are being made to explore a compensated quota trading mechanism to enhance the carbon market’s price discovery function.

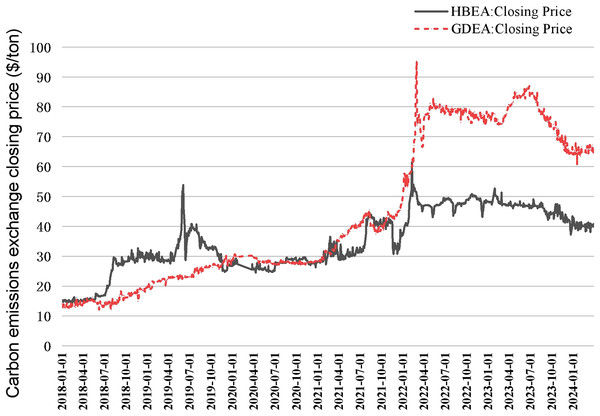
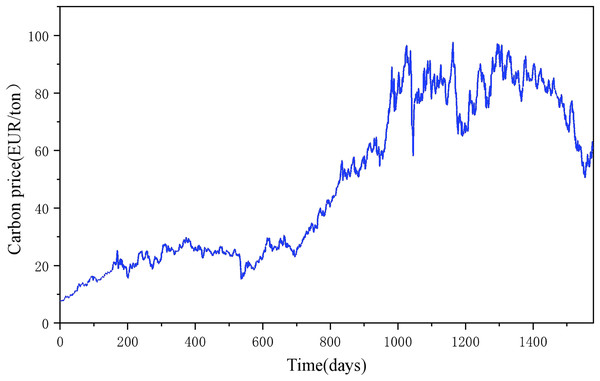
In Table 1 it can be seen that Hubei and Guangzhou carbon emission rights exchanges have significant advantages in terms of trading volume, trading turnover, market mechanism, and innovative initiatives, reflecting their important position and influence in China’s carbon market (Liu, Jiang & Ye, 2020; Liu, Ma & Wang, 2015). Therefore, this article collects Hubei and Guangzhou carbon market data from CHOICE Financial Terminal (Fig. 2), which helps to comprehensively understand and analyze the carbon emission right trading price and its influencing factors.

Table 1:

Comparative data of eight major carbon emission rights exchanges in China.

Carbon exchange	Area	Established year	Annual trading volume (10,000 tons)	Annual trading amount (100 million yuan)	Main traded varieties	Trading mechanism	Policy support	Innovative measures
Beijing	North China	2013	500	50	Carbon emissions rights	Spot trading	Strong	Few
Shanghai	East China	2013	600	60	Carbon emissions rights	Spot trading	Strong	Few
Tianjin	North China	2013	550	55	Carbon emissions rights	Spot trading	Strong	Few
Chongqing	South- west	2013	450	45	Carbon emissions rights	Spot trading	Medium	Few
Shenzhen	South China	2013	700	70	Carbon emissions rights	Spot trading	Strong	Few
Fujian	East China	2016	300	30	Carbon emissions rights	Spot trading	Medium	Few
Guangzhou	South China	2013	800	80	Carbon emissions rights, carbon forwards	Spot, forward	Strong	Many
Hubei	Central China	2014	750	75	Carbon emissions rights	Spot, auction	Strong	Many

DOI: 10.7717/peerj-cs.2827/table-1

Note:

Data source: annual reports of the exchanges (2023). Results with significant advantages are shown in bold.

Variable selection and data sources

In this article, the carbon market price of Hubei Province and Guangzhou City is selected as the dependent variable, and the historical carbon price as well as a variety of domestic and international influencing factors are used as independent variables for empirical analysis. The data used covers the daily data from January 1, 2018, to March 31, 2024, which are all derived from the Choice Financial Terminal database. In the process of data selection, the effects of domestic and international public holidays, differences in trading hours, and missing values of variables are especially considered. In addition, to extract the time series characteristics of the carbon price data, this article converts the raw data into a stacked data type and incorporates the sliding window method for forecasting. Specifically, assuming that the target of prediction is the carbon price at the t+3th moment, the input data will include continuous observations from the t-10th moment to the t-th moment (Li, Liang & Zhou, 2016). In this study, the size of the sliding window is set to five quarters, i.e., data from the first five quarters (January 1, 2018, to March 31, 2019) are used as the training set to predict the carbon price in the sixth quarter (April 1, 2019, to June 30, 2019). A series of overlapping sample datasets are created by moving the data backward quarter by quarter, with each move having a step size of one quarter. The exact structure of the sliding window is shown in Fig. 3.

Data pre-processing

There are different magnitudes and units between the collected data on the impact factors, to make the data more comparable, the data need to be linearly normalized to convert the data to the same magnitude or unit, so that it can be easily compared and analyzed and also can improve the accuracy and effectiveness of the machine learning algorithms. The expression for normalization is as follows:

(23) $$\begin{array}{c}{\mathrm{x}}^{\ast }={\displaystyle \frac{\mathrm{x}-{\mathrm{x}}_{\mathrm{m}\mathrm{i}\mathrm{n}}}{{\mathrm{x}}_{\mathrm{m}\mathrm{a}\mathrm{x}}-{\mathrm{x}}_{\mathrm{m}\mathrm{i}\mathrm{n}}}}\end{array}.$$

Among them, ${\mathrm{x}}^{\ast }$ represents the normalized value; $\mathrm{x}$ is the original data, ${\mathrm{x}}_{\mathrm{m}\mathrm{i}\mathrm{n}}$ is the minimum value in the dataset, and ${\mathrm{x}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ is the maximum value in the dataset. After normalization, the data falls within the range of [0, 1].

Establishment of the ultimate indicator system

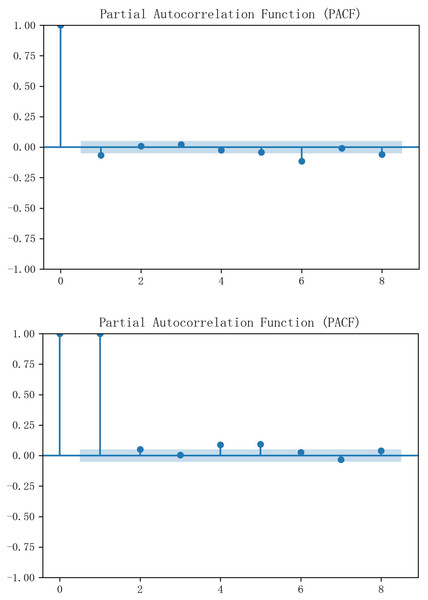
The economists David Dickey and Wayne Fuller proposed the Augmented Dickey-Fuller (ADF) test in 1979. The test is a statistical method used to test whether the time series data has a unit root, i.e. to verify whether the data is smooth. Through the ADF test, it can be obtained that the p-value of Hubei is 0.252318 and the p-value of Guangzhou is 0.766068, both of which are larger than the usually chosen significance level (e.g., 0.05 or 0.01), and therefore the original hypothesis cannot be rejected, i.e., neither of the two carbon markets’ historical carbon price data has smoothness. After one difference was performed separately, the data had all been smooth, and partial autocorrelation analysis was subsequently introduced to select the input historical characteristics for the prediction method. Figure 4 demonstrates the PACF results, and it can be seen that both Hubei and Guangzhou carbon price data have significant third-order autocorrelation. ${\mathrm{x}}_{\mathrm{i}}$ is the output feature, and { ${\mathrm{x}}_{\mathrm{i}-1}$, ${\mathrm{x}}_{\mathrm{i}-6}$, ${\mathrm{x}}_{\mathrm{i}-8}$} is determined as the input historical variable of Hubei carbon price. { ${\mathrm{x}}_{\mathrm{i}-1}$, ${\mathrm{x}}_{\mathrm{i}-4}$, ${\mathrm{x}}_{\mathrm{i}-5}$} is identified as the input historical variable of Guangzhou carbon price.

More input features may reduce the prediction accuracy due to redundancy. Identifying and screening out the most effective variables can not only achieve the goal of dimensionality reduction but also effectively avoid the problem of multicollinearity among data, thus improving the prediction performance of the model. Therefore, to identify the main external influences affecting carbon prices in Hubei and Guangzhou, this article adopts the Lasso regression algorithm for feature selection.

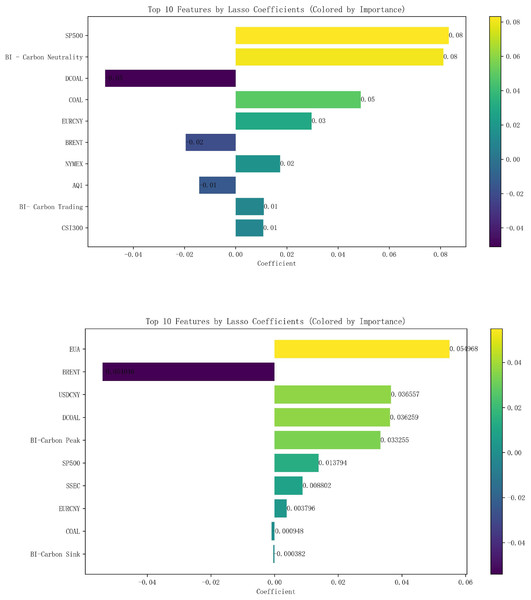
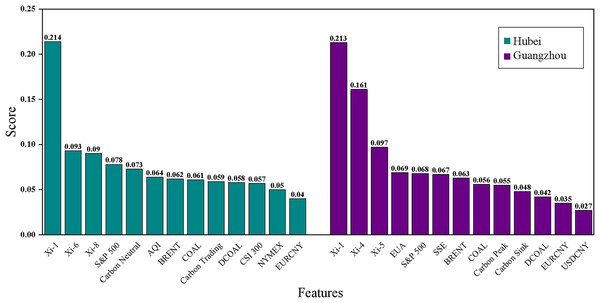
After normalizing all the data, Lasso regression analysis was carried out with the 16 external influences listed in Table 2 as independent variables and carbon emissions as dependent variables, with the parameter K value taken as 0.01. The correlation analysis shows that the top 10 variables in terms of carbon price correlation in Hubei Province are the S&P 500, Baidu index-Carbon Neutral, Coking Coal Futures Clearing Price, Power Coal Futures settlement price, EURCNY, Brent crude oil futures settlement price, NYMEX natural gas futures closing price, AQI, Baidu index-carbon trading, CSI 300 index, and the top 10 carbon price-related variables in Guangzhou are EUA, Brent crude oil futures settlement price, USDCNY, Power Coal Futures Settlement Price, Baidu index-Carbon Peak, S&P 500 Index, SSE Composite Index, EURCNY, Coking Coal Futures Settlement Price, and Baidu search index-Carbon Sinks, as shown in Fig. 5, whereby they are identified as the 10 key influencing factors affecting the carbon price in Hubei Province and Guangzhou City, respectively.

Evaluation indicators

In this article, mean square error (MSE), mean absolute error (MAE), mean absolute percentage error (MAPE) and coefficient of determination (R-squared or R²) are used as indicators to assess the prediction performance of the model. The MSE is the average of the square of the differences between the predicted values and the actual values, while the MAE measures the average size of the absolute size of the differences between the predicted values and the actual observations, visualizing the average level of prediction error. The MAE visualizes the average level of prediction error by measuring the average size of the absolute difference between the predicted value and the actual observed value. On the other hand, the R² metric quantifies the goodness of fit or correlation between the model’s predictions and observations. The formula for each indicator is shown in Table 3.

Model parameter setting

To verify the prediction accuracy of the COA-XGBoost-CEEMDAN model, various comparison algorithms are used to analyze the prediction effect. For the base model prediction, GBDT, support vector machine (SVR), and XGBoost models are selected to compare and analyze the prediction effect of COA-XGBoost; for the residual correction combination model prediction, the residual sequences generated by GWO-XGBoost are compared and decomposed using VMD and CEEMDAN methods. The parameter settings and optimal parameters of each model are shown in Table 4, and the rest of the parameters are set using Python default parameters.

Experiment 1: Results of carbon price prediction in Hubei Province

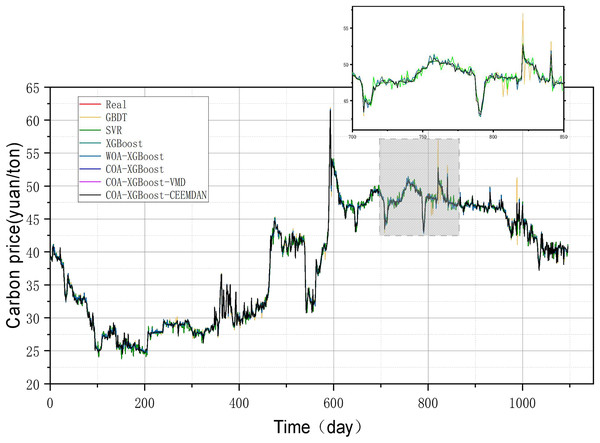
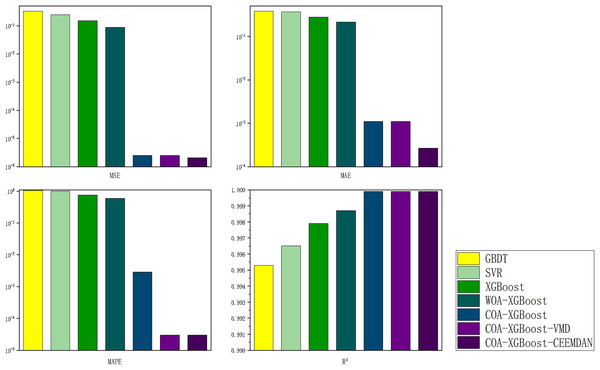
The evaluation metrics of the established prediction framework and other prediction models are shown in Table 5 and Fig. 6, and the comparison of the predicted values of different models is shown in Fig. 7. The values with the best results in Table 5 will be bolded, and Fig. 6 visualizes the prediction performance of each model in the form of bar charts. The experimental data show that the model proposed in this article outperforms the other compared models in all cases. The following conclusions can be drawn.

(1) The prediction model proposed in this article outperforms other models in any comparison of evaluation metrics. According to the results listed in Table 5, the MSE, MAE, MAPE, and R² of the designed forecasting framework are 2.0573e−06, 0.000268, 0.00003, and 0.9999, respectively.

(2) When comparing the single model XGBoost and XGBoost with the cheetah optimization algorithm added, it is found that the model with the Cheetah optimization algorithm added is more accurate. The four evaluation metrics of MSE, MAE, MAPE, and R² for the XGBoost model are 0.1536, 0.2788, 0.7580 and 0.9979, respectively. The values of COA-The values of the four evaluation metrics of XGBoost are 2.4796e−06, 0.0011, 0.0029, and 0.9999, which are 99.9%, 99.6%, 99.6%, and 0.2% respectively, compared to the metrics of XGBoost. It can be seen that the accuracy of the model with the addition of the optimization algorithm has been improved to some extent.

(3) The single model without the decomposition algorithm added is compared with the model incorporating the decomposition algorithm, which has better prediction results. The COA-XGBoost model with the CEEMDAN decomposition algorithm incorporated has values of 2.0573e−06, 0.000268, 0.00003, 0.9999, and the percentage improvement of the four metrics are 17.0%, 75.6%, 99.0%, and 0.000001%, which is a substantial improvement in accuracy. The contribution of the CEEMDAN algorithm to the prediction results is shown.

Experiment 2: Results of carbon price prediction in guangzhou

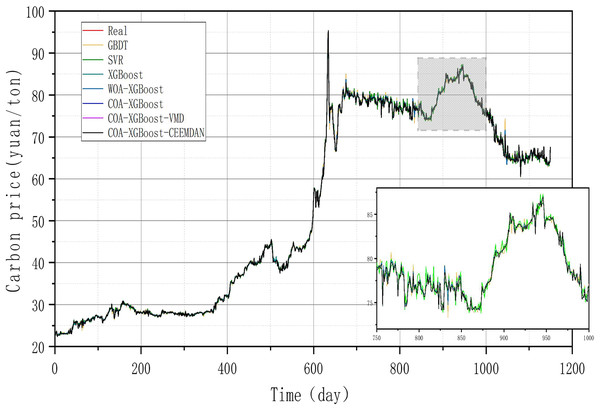
To prove the robustness of the model, a further carbon market in Guangzhou will be selected for an experimental study. Taking the relevant data of the Guangzhou carbon market as a sample, the prediction results of each model are shown in Table 6 and Fig. 8, and the line graph comparing the predicted values of different models is shown in Fig. 9. It can be summarized from numeral charts that Experiment 2 has the same conclusion as Experiment 1. It shows that the model proposed in this article combines the advantages of optimization algorithm, decomposition algorithm, and feature selection, and performs well in all aspects.

Importance analysis of carbon price characteristics

Characteristic importance analysis can help the government to make scientific decisions in various aspects such as an in-depth understanding of the energy market, optimizing policy design, and formulating cross-cutting policies by identifying the factors that have an important impact on the target value of the forecast (Chang & Park, 2023). In this article, the Lasso regression model is used for feature importance analysis. The results of the feature importance ranking of each model are shown in Fig. 10 and Table 7. Analyzing the feature ranking in Table 7, it is found that the historical carbon price is the best data source for predicting the carbon price in these two carbon markets, which is because the price time series is a comprehensive external manifestation of the intrinsic complexity of the market, which contains important information about the past market performance and price fluctuations, and can help researchers to analyze and predict through these historical price data. Additionally, it can be observed that the settlement price of Brent crude oil futures in the energy factors and the S&P 500 index in the macroeconomic factors rank among the top in both datasets, making them key external factors in carbon price prediction.

Experiments on the application of the model

EU carbon price forecasts

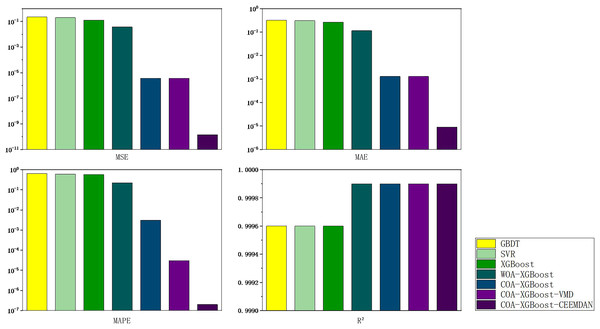
To explore the generalization ability of the proposed model and the generalizability of the study, price forecasts for the EU carbon market are added. An indicator system is established by considering international carbon prices, macroeconomics, energy prices, climatic conditions, macro-policy and emerging media indices, and historical prices. The daily trading data of EUA from January 1, 2018 to March 31, 2024, is selected for forecasting. There are 1,577 data in total. As shown in Fig. 11, the carbon price experienced a typical price change pattern during the training period, including the three stages of rise, fall, and oscillation. The results of the metric calculations for each of the models are shown in Table 8, with the best data in the table shown in bold.

Table 8:

The forecasting results for the EU dataset.

Models	MSE	MAE	MAPE	R²
GBDT	0.8679	0.5725	1.0009	0.9986
SVR	0.5923	0.5087	0.9065	0.9991
XGBoost	0.3620	0.4593	0.9585	0.9994
WOA-XGBoost	0.2370	0.3284	0.5833	0.9996
COA-XGBoost	1.6563e−05	0.0028	0.0063	0.9999
COA-XGBoost-VMD	1.6417e−05	0.0028	0.00006	0.9999
COA-XGBoost-CEEMDAN	1.2653e−07	0.0003	0.000006	0.9999

DOI: 10.7717/peerj-cs.2827/table-8

Note:

The best result is shown in bold.

According to Table 8, the following conclusions can be obtained. First, COA-XGBoost with optimization algorithm added has an excellent performance in a single machine learning model, and the evaluation indexes are improved by 99.99%, 99.39%, 99.34%, and 0.05% respectively compared with XGBoost without optimization algorithm added. From this, it can be concluded that using COA to optimize the parameters of XGBoost can improve the prediction accuracy. Secondly, the accuracy of the hybrid algorithm with the addition of VMD and CEEMDAN is significantly improved, CEEMDAN presents a small increase compared to the VMD basis, and the evaluation indexes of COA-XGBoost-CEEMDAN reach 1.2653e−07, 0.0003, 0.000006, and 0.9999, respectively. Through the preliminary decomposition of the predicted residual sequences, effective information is extracted, which further improves the accuracy of prediction.

In summary, the model proposed in this article shows the same excellent results in the prediction of the EU carbon trading market compared with several other models, which proves the generalization ability of this model and can be better applied to new data, indicating its universality and reliability.

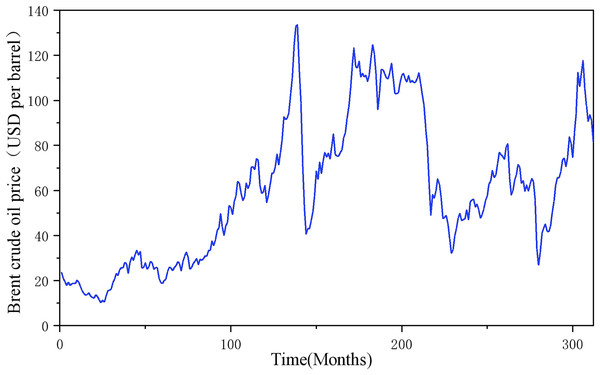
Oil price forecasts

To further verify the generalization performance of this model in heterogeneous energy markets, this study extends the prediction scenario to the international crude oil market. Based on the multi-scale coupling characteristics of the global energy market, a system of indicators covering commodity attributes, economic factors, alternative energy sources and geopolitical factors, as well as its own historical prices, is constructed. All indicators are based on monthly data with the time interval from January 1997 to December 2022, totaling 212 data, as shown in Fig. 12. The Lasso-COA-XGBoost-CEEMDAN model proposed in this article is used to predict the forecast of Brent oil price, and the model performance is quantified by a quadratic evaluation system: MSE = 0.1553, MAE = 0.3544, MAPE = 0.0058 and R² = 0.9997. The results show that the model also exhibits excellent predictive performance in crude oil price forecasting.

Comparison between the proposed model and other models

In recent years, there have been numerous studies on carbon prices. To prove the validity of the proposed model, this article compares other hybrid models for carbon price forecasting. The comparison models are described as follows:

Ke et al. (2023) proposed multi-decomposition-XGBoost model. It combines the results of the first and second decompositions based on sample entropy, then performs another round of decomposition and uses the XGBoost prediction model to make predictions, and finally, summarizes the results to obtain the carbon price combination prediction.

Hu & Cheng (2023) developed the SD-RE-MIC-SSA-HKELM-Ensemble model to forecast carbon price. It utilizes variational mode decomposition (VMD) to decompose the carbon price into several modes and then reconstructs these modes using polar entropy. The multifactor HKELM optimized by the sparrow search algorithm is used to forecast the reconstructed subsequences, and the main external factors and the historical time series data of carbon price innovatively selected by the information coefficient maximization method are used as the input variables of the forecasting model. Finally, a nonlinear integrated learning method is introduced to determine the residual term and the predicted value of the final carbon price.

The above hybrid models present innovative approaches in the field of carbon price forecasting research and advance the field of carbon price forecasting. By comparing with these models, the performance of the proposed model in predicting carbon price can be evaluated. The proposed model and the compared models are compared by three evaluation indexes, RMSE, MAE, and MAPE, and the results are shown in Table 9, with the optimal results shown in bold. Meanwhile, to ensure the rigor of the comparison, the time horizon of the prediction is adjusted to be consistent. The time range of the Hubei carbon market is from August 1, 2018 to November 13, 2020, and the time range of the dataset of the Guangzhou carbon market is from January 3, 2017 to February 28, 2022.

After comparative analysis with other models, it is found that the model proposed in this study presents superior performance performance. As can be seen from Table 9, hybrid models have been widely used and highly matured in the field of carbon price forecasting, by combining different types of forecasting models to better integrate the advantages of the models and improve the forecasting accuracy. In the comparison of forecasting in the Hubei carbon market, the RMSE, MAE, and MAPE of the model proposed in this article reach 0.002%, 0.0004%, and 0.16%, respectively, and the values of all evaluation indexes are better than those of the comparison model. In the comparison experiment of the Guangzhou carbon market, the comparative model’s indicators are 0.1716%, 0.1218%, and 0.26%, and the RMSE and MAE performance is not as good as the performance of the model proposed in this article, though. None of the above comparative models have made split-frequency predictions of the residual series or considered the influence of extreme events, which are possible reasons why the prediction accuracy cannot be improved. None of the above comparative models performs split-frequency prediction on the residual series, ignoring the rich information contained in the residuals, and does not take into account the impact of extreme events, which makes the model lack of adaptability and robustness in the face of such special cases, and these are the reasons that may lead to the failure to improve the prediction accuracy.

Limitations and future directions of work

In this article, a novel carbon price prediction method is proposed, which significantly improves the prediction accuracy and thus assists governments, enterprises, and investors in making more accurate decisions. Although the results of the study show good prediction results, there are still some limitations. In terms of the model: (1) The heuristic optimization algorithm used is more complicated in terms of parameter configuration. Determining the appropriate parameters not only requires a lot of time and computational resources, but also this complex parameter adjustment process restricts the enhancement of the model’s intelligence level to a certain extent, which reduces the convenience and efficiency of the model application. (2) Although the CEEMDAN method is used to decompose the residual series, it is limited to a single decomposition, which may not be able to fully capture the deeper nonlinear features. In the study of the carbon price problem: (1) This study only realizes a single-step forecast and fails to comprehensively analyze the future carbon price trend from a more macroscopic perspective. (2) The characteristics of carbon price influencing factors over time are neglected.

Based on the above limitations, future research work can be carried out in the following directions: firstly, in-depth research should be carried out on the optimization algorithm and model streamlining, a more intelligent and convenient prediction model should be constructed, the automation of the parameter setting of the heuristic optimization algorithm should be realized, and the complexity of the experimental steps should be reduced, so as to improve the operation efficiency and application popularization of the model. Secondly, the introduction quadratic decomposition in the residual sequence processing should be attempted to fully reveal the deep nonlinear relationship and make the model prediction more accurate. Finally, the carbon price prediction method in this study can be extended and applied to other related fields, such as energy market prediction and climate change risk management, which will verify the generalizability and application value of the research results.

Policy recommendations

As one of the world’s largest carbon emitters, establishing a robust carbon market in China will have a positive impact on reducing global carbon emissions. The following related policy recommendations are proposed based on the research findings of this article:

(1) As a key indicator for predicting future carbon prices, historical carbon prices provide extremely valuable information about their trends and patterns. Therefore, the government should first set up a carbon market reserve mechanism to put in or recover carbon quotas at the right time according to the market condition, to ensure the stability of carbon market prices and prevent drastic fluctuations. In addition, the government should also build a complete carbon market database, including historical prices, trading volume, and emission data of various carbon markets, to facilitate researchers’ access to relevant information for in-depth analysis and research.

(2) Fluctuations in energy prices are directly related to the production costs and energy choices of enterprises, which have a complex impact on carbon prices. For the Hubei carbon market, coal prices and power coal prices have a high impact score on carbon price forecasts. For the Guangzhou carbon market, crude oil prices and power coal prices have higher impact scores on carbon price forecasts. The government should take several measures to reduce the burden of production costs on enterprises when energy prices rise. Firstly, the government should support companies in improving energy efficiency and technology upgrades through financial subsidies and soft loans. Second, it should actively promote the development of clean energy, increase the supply of clean energy, and reduce reliance on coal and oil, thereby reducing the volatility of carbon prices and their impact on traditional energy prices. When energy prices fall, the government needs to review and adjust the carbon quota allocation mechanism to ensure that the carbon market still incentivizes companies to adopt low-carbon production and business strategies. For the Guangzhou carbon market in particular, to ensure the accuracy of carbon price forecasts and promote sustainable economic development, the government needs to pay close attention to the price movements of natural gas and coal.

(3) On the economic front, the Hubei carbon market should monitor the price movements of the S&P 500, the EUR-RMB exchange rate, and the CSI 300, and the Guangzhou carbon market should pay attention to the price movements of the USD-RMB exchange rate, the S&P 500, the SSE Composite Index and the EUR-RMB exchange rate, which are of reference value in accurately forecasting carbon market prices. When these indices rise, it indicates optimism in the stock market and expansion of economic activity, which may increase demand for the carbon market. The government should capitalize on periods of economic prosperity to strengthen training and education efforts related to the carbon market, raise awareness of the carbon market among enterprises and investors, and promote active trading in the market. Additionally, when indicators are falling, the government should take measures to stimulate economic growth and promote the sustainable development of a low-carbon economy. To lessen the detrimental effects of exchange rate swings on the economy and the energy market, the government must also keep the currency rate reasonably constant.

(4) To better grasp the public’s concern and the trend of public opinion on the carbon market and related issues, the government should make full use of big data tools such as the Baidu index. The Hubei carbon market should monitor the trends of the keywords “carbon neutral” and “carbon trading”, and the Guangzhou carbon market should pay attention to the trends of the keywords “carbon peak” and “carbon sink”. The Guangzhou carbon market should focus on the trends of the keywords “carbon peak” and “carbon sink”, which have reference values for accurate prediction of carbon market price. By monitoring the trend of keyword searches related to the carbon market, the government can keep abreast of changes in the public’s interest in carbon emissions and carbon trading, and provide a basis for developing more targeted publicity and education programs. In addition, changes in the Baidu index can also reflect market expectations and public sentiment, helping to warn of potential market fluctuations in advance and assisting policymakers in making more scientific and rational decisions.