RBI: a novel algorithm for regulatory-metabolic network model in designing the optimal mutant strain

The implementation of reliability theory in metabolic engineering

The RBI algorithm operated reliability theory to determine the reliability value of metabolic genes or reaction fluxes. To calculate the reliability value, the Boolean rules outlined in the empirical GRNs and GPRs must be considered. The Boolean rules governing the empirical GRNs consist of three operators: NOT, AND, and OR. The NOT operator indicates that transcription factors (TFs) associated with this operator inhibit the regulated genes. Suppose that the $i$th transcription factor and the $j$th metabolic gene are denoted by TF_i and MG_j, respectively. Several rules must be considered when determining the reliability value of MG_j ( $r_{\mathrm{M}{\mathrm{G}}_j}$) regulated by TF_i, as outlined in the following numbering.

1. If MG_j is only regulated by TF_i involving the NOT operator, i.e., MG_j = NOT TF_i, then the reliability value of MG_j is determined by Eq. (2). (2) $$r_{\mathrm{M}{\mathrm{G}}_j}=p_{\mathrm{T}{\mathrm{F}}_i}^c$$where $p_{\mathrm{T}{\mathrm{F}}_i}^c$ is the complement of $p_{\mathrm{T}{\mathrm{F}}_i}$, which is the probability value of TF_i being active. If TF_i is knocked out, then $p_{\mathrm{T}{\mathrm{F}}_i}=0$.

2. If MG_j is regulated by TF_h and TF_i involving the AND operator, i.e., MG_j = TF_h AND TF_i, then based on the formula of series structure in reliability theory, the reliability value of MG_j is determined by Eq. (3). (3) $$r_{\mathrm{M}{\mathrm{G}}_j}=p_{\mathrm{T}{\mathrm{F}}_h}.p_{\mathrm{T}{\mathrm{F}}_i}.$$

   The series structure is used in this case due to the same characteristic between the AND operator and this structure.

3. If MG_j is regulated by TF_h and TF_i involving the OR operator, i.e., MG_j = TF_h OR TF_i, then based on the formula of parallel structure in reliability theory, the reliability value of MG_j is determined by Eq. (4). (4) $$r_{\mathrm{M}{\mathrm{G}}_j}=1-(1-p_{\mathrm{T}{\mathrm{F}}_h})(1-p_{\mathrm{T}{\mathrm{F}}_i}).$$

   The use of parallel structure in this case is also based on the same reasons as the previous operator.

For instance, aspA, one of the metabolic genes of E. coli type strain iAF1260 is regulated by two TFs, Crp and FnR, whose Boolean rules are shown in Eq. (5).

(5) $$aspA=(Crp\mathrm{A}\mathrm{N}\mathrm{D}\left(\mathrm{N}\mathrm{O}\mathrm{T}\mathrm{F}\mathrm{n}\mathrm{r}\right))\mathrm{O}\mathrm{R}\mathrm{F}\mathrm{n}\mathrm{r}.$$

There are three operators involved in regulating aspA, namely NOT, AND, and OR. The reliability value of aspA ( $r_{aspA}$) can be determined using the three previously established reliability calculation rules. The illustration of transcription factors regulating the aspA gene in a series-parallel structure is in Fig. S3. The steps to get the $r_{aspA}$ formula are elaborated in Eq. (6).

(6) $$\begin{array}{rl}{r}_{aspA}=& (Crp\mathrm{A}\mathrm{N}\mathrm{D}\left(\mathrm{N}\mathrm{O}\mathrm{T}\mathrm{F}\mathrm{n}\mathrm{r}\right))\mathrm{O}\mathrm{R}Fnr\\ =& (p_{Crp}\mathrm{A}\mathrm{N}\mathrm{D}{\mathrm{p}}_{Fnr}^{\mathrm{c}})\mathrm{O}\mathrm{R}{\mathrm{p}}_{Fnr}\\ =& 1-(1-p_{Crp}.p_{Fnr}^c)(1-p_{Fnr}).\end{array}$$

The same procedure is utilized to determine the reliability value of flux reactions catalyzed by metabolic genes outlined in the GPR rules on GSMMs. The ATP synthase reaction, ATPS4r, is a flux reaction in strain iAF1260, catalyzed by three metabolic genes: AtpF0, AtpF1, and AtpI, as indicated by the boolean rule in Eq. (7).

(7) $$ATPS4r=(AtpF0\mathrm{A}\mathrm{N}\mathrm{D}AtpF1)\mathrm{O}\mathrm{R}(AtpF0\mathrm{A}\mathrm{N}\mathrm{D}AtpF1\mathrm{A}\mathrm{N}\mathrm{D}AtpI).$$

The illustration of the metabolic gene structure that catalyses the reaction flux ATPS4r has been presented in the Fig. S4. The method for acquiring $r_{ATPS4r}$ is outlined in Eq. (8).

(8) $$\begin{array}{rl}{r}_{ATPS4r}& =(AtpF0\mathrm{A}\mathrm{N}\mathrm{D}AtpF1)\mathrm{O}\mathrm{R}(AtpF0\mathrm{A}\mathrm{N}\mathrm{D}AtpF1\mathrm{A}\mathrm{N}\mathrm{D}AtpI)\\ & =(p_{AtpF0}\mathrm{A}\mathrm{N}\mathrm{D}{\mathrm{p}}_{AtpF1})\mathrm{O}\mathrm{R}({\mathrm{p}}_{AtpF0}\mathrm{A}\mathrm{N}\mathrm{D}{\mathrm{p}}_{AtpF1}\mathrm{A}\mathrm{N}\mathrm{D}{\mathrm{p}}_{AtpI})\\ & =(p_{AtpF0}.p_{AtpF1})\mathrm{O}\mathrm{R}({\mathrm{p}}_{AtpF0}.{\mathrm{p}}_{AtpF1}.{\mathrm{p}}_{AtpI})\\ & =1-(1-p_{AtpF0}.p_{AtpF1})(1-p_{AtpF0}.p_{AtpF1}.p_{AtpI}).\end{array}$$

The calculations presented will be utilized for all genes regulated by TFs in GRNs to determine their reliability values. Also, the reliability value of reaction flux based on the GPR rules is calculated using the same procedure. Subsequently, those reliability values obtained will be used to establish soft constraints for the regulatory-metabolic networks model, aiming to identify optimal mutant strains.

The reliability-based integrating algorithm

This study presents a novel algorithm for constructing a regulatory-metabolic network model. This approach aims to establish a comprehensive pipeline linking GRNs and metabolic networks that incorporates the interaction types between various genes in GRNs and GPRs, a gap not addressed by existing algorithms. The algorithm proposed is the reliability-based integrating (RBI) algorithm. The reliability theory is applied in RBI to address the Boolean rules found in the empirical GRNs and GPR rules.

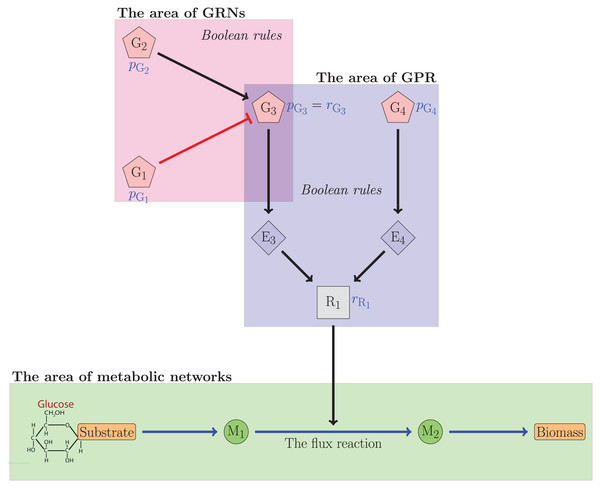
Figure 1 illustrates the relationship between gene regulatory networks and metabolic networks. In the figure, the $i$th gene was denoted by ${\text{G}}_i,\mathrm{\forall }i\in \{1,2,3,4\}$. The $j$th enzyme was denoted by ${\text{E}}_j,\mathrm{\forall }j\in \{3,4\}$. The $k$ metabolite was denoted by ${\text{M}}_k,\mathrm{\forall }k\in \{1,2\}$. Meanwhile, R₁ was the reliability value of the flux reaction catalyzed by G₃ and G₄. The figure indicated that G₃ was regulated by G₁ and G₂, which respectively inhibited and activated G₃. The reliability value of G₃ can be determined from this interaction. The reliability value of R₁ was subsequently calculated using the Boolean equation involving G₃ and G₄. The reliability value of the flux reactions will be used to establish regulatory constraints governing the flux reaction. In this case, the reliability theory is utilized to compute $r_{{\mathrm{G}}_3}$ and $r_{{\mathrm{R}}_1}$.

Three types of RBI algorithms have been proposed in this study, namely RBI-T1, RBI-T2, and RBI-T3. The distinction is in establishing the initial probability value of TFs. The RBI-T1 algorithm assumes that TFs that are not knocked out have the same probability of being in active or inactive conditions. Consequently, the initial probability value of TFs in this algorithm is set to 0.5. The initial probability values of RBI-T2 and RBI-T3 are based on gene expression data. The RBI-T2 algorithm utilizes the binarization process from the PROM algorithm to derive the probability of active transcription factors (TFs). The initial probability value of RBI-T3 is derived from the average of the initial probability values of RBI-T1 and RBI-T2. The formula to get the initial probability values of transcription factors for each type of RBI algorithm is presented in Table S1.

Furthermore, the RBI algorithm considers three parameters: $\alpha$, $\beta$, and $\gamma$. The $\alpha$ parameter is derived from the binarization of gene expression data to establish the initial values of transcription factors for RBI-T2 and RBI-T3. This parameter is used to acquire information regarding the probability value of genes as transcription factors in an active state, utilizing the abundance of gene expression data measured under diverse environmental conditions and genetic perturbations (Chandrasekaran & Price, 2010). Additionally, the $\beta$ and $\gamma$ parameters are utilized by RBI-T1, RBI-T2, and RBI-T3 to model the partial effects experienced by various reactions as a result of the influence of genes or transcription factors (Raman, 2021; Simeonidis, Chandrasekaran & Price, 2013). The block diagram of the RBI procedure is available in Fig. S5. The technical steps of this algorithm are outlined below.

1. Input data required, namely GSMMs, GRNs, and the gene expression data.

2. Choose the TFs to be knocked out.

3. Determine the initial probability value of TF_i, ∀i using Eq. (9). (9) $$p_{\mathrm{T}{\mathrm{F}}_i}=\{\begin{array}{cc}0\hfill & \mathrm{i}\mathrm{f}\mathrm{t}\mathrm{h}\mathrm{e}i\mathrm{t}\mathrm{h}\mathrm{T}\mathrm{F}\mathrm{i}\mathrm{s}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{c}\mathrm{k}\mathrm{e}\mathrm{d}\mathrm{o}\mathrm{u}\mathrm{t}\hfill \\ f(\mathrm{T}{\mathrm{F}}_i)\hfill & \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}.\hfill \end{array}$$

   Determining the value of $f(\mathrm{T}{\mathrm{F}}_i)$ is based on the RBI type. For RBI-T1, $f(\mathrm{T}{\mathrm{F}}_i)=0.5,\mathrm{\forall }i$. Furthermore, if RBI-T2 is used, the value of $f({\mathrm{T}\mathrm{F}}_i)$ is obtained from Eq. (10). (10) $$f(\mathrm{T}{\mathrm{F}}_i)=\frac{1}{d}\times n(\mathrm{T}{\mathrm{F}}_i=1).$$where $n({\mathrm{T}\mathrm{F}}_i=1)$ refers to the number of ‘1’ values in the gene expression data that has been transformed to binary form based on the parameter $\alpha$ and the binarization procedure of the PROM algorithm (Chandrasekaran & Price, 2010; Ananda, Daud & Zainudin, 2024); meanwhile, $d$ is the dimension of the gene expression data used. Moreover, $f(\mathrm{T}{\mathrm{F}}_i)$ of RBI-T3 is obtained from the average value of $f(\mathrm{T}{\mathrm{F}}_i)$ obtained by RBI-T1 and RBI-T2, the formula is presented in Eq. (11).

   (11) $$f(\mathrm{T}{\mathrm{F}}_i)=\frac{1}{2}(0.5+\frac{1}{d}\times n(\mathrm{T}{\mathrm{F}}_i=1)).$$

4. Calculate $r_{\mathrm{M}{\mathrm{G}}_j},\mathrm{\forall }j$, namely the reliability value of the $j$th metabolic gene, using the reliability theory formula.

5. Define the probability value of the metabolic genes obtained from their reliability values when those genes are regulated by their respective TFs. However, if there is no information that TFs regulate metabolic genes, their probability is one.

6. Calculate $r_{\mathrm{R}{\mathrm{F}}_k},\mathrm{\forall }k$, namely the reliability value of the $k$th reaction flux, using the reliability theory formula.

7. Determine the reference flux using flux variability analysts (FVA). We obtain [ ${\text{lb}}_k^{\ast }$, ${\text{ub}}_k^{\ast }$], $\mathrm{\forall }k$ which is the bounds of the $k$th reaction flux.

8. Generate regulatory constraints into the model by updating the bounds of reaction fluxes (RF) that are not transport reactions or ‘ATPM’ reactions and whose reliability values are less than or equal to $\beta$. The formula used to update the bounds of the $k$th reaction flux, $\mathrm{\forall }k$, is shown in Eq. (12). (12) $$\begin{array}{rl}\mathrm{u}{\mathrm{b}}_k& =r_{\mathrm{R}{\mathrm{F}}_k}\times {\mathrm{u}\mathrm{b}}_k^{\ast }+\gamma .\\ \mathrm{l}{\mathrm{b}}_k& =r_{\mathrm{R}{\mathrm{F}}_k}\times {\mathrm{l}\mathrm{b}}_k^{\ast }-\gamma .\end{array}$$where $\gamma$ refers to the soft constraint adopted from the PROM algorithm (Chandrasekaran & Price, 2010).

9. Determine the optimal reaction flux using the FBA algorithm.

10. The optimal flux distribution is obtained.

The dataset used

To validate the performance of the proposed RBI algorithms, a simulation of metabolic engineering was performed using those algorithms on E. coli and S. cerevisiae. The results were compared with empirical data and previous literature demonstrating the potential mutant strains for the overproduction of desired metabolites. The computational simulation conducted utilized genome-scale metabolic models (GSMMs), regulatory networks (GRNs), and gene expression data as datasets.

The performance measurements

Performance measurements are essential for assessing the efficacy of the proposed RBI algorithms. The simulations assessed both effectiveness and efficiency. The validation applied to assess these two aspects is outlined in the subsequent discussion.

The optimal parameters of the RBI algorithm

The RBI algorithms necessitate three parameters ( $\alpha$, $\beta$, and $\gamma$), which emerge from uncertainties in genes or reaction fluxes. Variability in gene expression significantly impacts cellular function. It arises from various factors, including stress response, pathogenesis, metabolism, development, cell cycle, circadian rhythms, and ageing (Raj & Van Oudenaarden, 2008). RBI-T2 and RBI-T3 use the $\alpha$ parameter to model uncertainties and derive initial quantity measures of regulatory gene expression or TFs from gene expression data, utilizing the binarization procedure of the PROM algorithm (Chandrasekaran & Price, 2010). The values serve as initial probability values for transcription factors in the RBI algorithm. Then, the $\beta$ and $\gamma$ parameters are utilized due to the reality that numerous genes/transcription factors may exert only a partial influence on reaction fluxes (Raman, 2021). The parameter $\beta$ quantifies the extent of enzyme performance generated by metabolic genes in affecting the activation energy of a flux reaction (Urry et al., 2017). Meanwhile, $\gamma$ serves as a partial effect for the bounds of flux reactions.

To obtain the optimal parameters required by RBI, various metaheuristic optimization techniques were operated, such as particle swarm optimization (PSO), genetic algorithm (GA), simulated annealing (SA), differential search algorithm (DSA), bijective-DSA (B-DSA), surjective-DSA (S-DSA), Elitist(1)-DSA (E1-DSA), Elitist(2)-DSA (E2-DSA), grey wolf optimization (GWO), whale optimization algorithm (WOA), genetic algorithm based on natural selection (GABONST), komodo mlipir algorithm (KMA), and Aquila optimizer (AO). Those selected metaheuristic optimisations were either state-of-the-art metaheuristic optimisation techniques or had been utilized in the design of the optimal mutant strain (Hor et al., 2024; Tan et al., 2023; Dzulkalnine et al., 2023; Suyanto, Ariyanto & Ariyanto, 2022; Abualigah et al., 2021; Lee et al., 2020; Albadr et al., 2020; Shen et al., 2019; Mirjalili & Lewis, 2016; Mirjalili, Mirjalili & Lewis, 2014). The fitness value was derived from the multiplicative inverses of the RMSE obtained.

Two microbial strains, E. coli and S. cerevisiae, have been used in simulations to determine the optimal parameters for each type of RBI. The results and gene knockout schemes for E. coli were presented by Covert et al. (2004), with biomass flux serving as the objective function. In S. cerevisiae, the production rates of succinate, 2, 3-butanediol, and ethanol were predicted and compared with previous literature (Shen et al., 2019). Those empirical results and validated TF knockout scheme were utilized to get the valid parameters for RBI, where to get the valid parameters, the empirical data was required Helbing (2010).

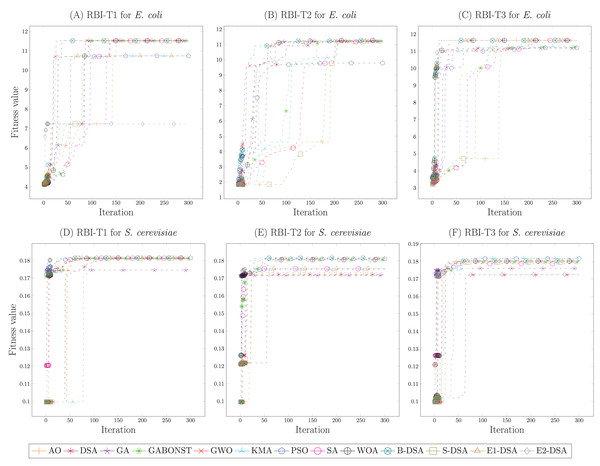
Figures 2A–2C demonstrated the simulation results of the E. coli strain each RBI type. From Fig. 2A, it could be known that the global convergence of B-DSA, GWO, S-DSA, DSA, WOA, and GABONST was similar enough. However, GWO precisely obtained the highest global convergence with a small difference; namely, its fitness value was 11.562. Then, in Fig. 2B, WOA received the highest global convergence of 11.269, demonstrating a small difference to SA, B-DSA, S-DSA, E1-DSA, KMA, GWO, GA, and GABONST. Afterward, the parameters achieved by the DSA algorithm for RBI-T3 were chosen because its algorithm provided the highest global convergence, namely 11.634. Accordingly, the optimal parameters of RBI-T1, RBI-T2, and RBI-T3 were respectively obtained from GWO, WOA, and DSA. Meanwhile, Figs. 2D–2F showed the simulation results of the S. cerevisiae strain in determining the optimal parameters of each RBI type. Based on the fitness value compared, it was concluded that the E1-DSA algorithm provided the best optimal parameters, where its fitness value of 0.1815 was the highest value. Furthermore, Figs. 2E and 2F showed that the B-DSA and KMA algorithms acquired the same and best global convergence, namely 0.182. Hence, the best optimal parameters for RBI-T1, RBI-T2, and RBI-T3 in the S. cerevisiae strain, respectively were obtained from E1-DSA, B-DSA, and KMA. Furthermore, the optimal parameters used in this study for each RBI type are presented in Table S3.

Performance of the RBI algorithm

The RBI algorithm was developed to integrate GRNs and metabolic networks by incorporating comprehensive Boolean rules from both GRNs and GPRs, including their interaction types. This algorithm enables researchers to assess the effectiveness of gene engineering approaches and determine the most effective mutant strategy for optimizing the desired metabolic flux. The designed mutant strains can be estimated in silico using RBI. The estimation results can subsequently be validated through actual TF knock-out and screening experiments conducted in the wet lab. The RBI algorithms were applied to estimate the outcomes of its gene engineering based on the actual results and prior literature, which were provided by Niu et al. (2021) and Shen et al. (2019).

The previous algorithms for the regulatory-metabolic network model were employed to compare and assess the RBI performance, specifically continuous-type models utilizing the empirical GRNs or the inferred GRNs. The advanced algorithms employed in the empirical GRNs were PROM and TRFBA. Simultaneously, recent algorithms utilizing the inferred GRNs, including TRIMER, OptRAM, and OptFlux, were utilized.

The time complexity

There are three types of the RBI algorithm, namely RBI-T1, RBI-T2, and RBI-T3. The difference between them is only in determining the probability value of the regulatory genes, $f(\mathrm{R}{\mathrm{G}}_i)\mathrm{\forall }i$. In computation, this difference does not have a significant effect on their processing time because the most complex type of RBI uses linear functions to determine the probability values of RG_i. The RBI algorithms utilize four pieces of information during its process: metabolic genes, regulatory genes, metabolic reactions, and metabolites. Suppose that the size of metabolic genes, regulatory genes, metabolic reactions, and metabolites in the dataset are $n_1,n_2,n_3$ and $n_4$, respectively. Subsequently, the time complexity of this algorithm based on big-O notation can be identified based on these sizes. The pseudocode of the RBI algorithm and its big-O notation in each step have been provided in Table S8.

Based on the dataset provided in the Table S2, it was known that the number of reactions, metabolites, and genes in the metabolic networks are not significantly different ( $n_1\approx n_3\approx n_4$). Meanwhile, the number of regulatory genes was quite below the number of metabolic genes, $n_2\le n_1$ (Shlomi et al., 2007). Suppose that $n$ is more or equal to $max\{n_1,n_2,n_3,n_4\}$. Subsequently, the time complexity can be estimated by referring to the size $n$, where the time complexity calculation procedure of the RBI algorithm could be conducted based on (Odhiambo Omuya, Onyango Okeyo & Waema Kimwele, 2021). Equation (17) showed the time complexity result of the RBI algorithm.

(17) $$\begin{array}{rlr}T(n)=& 2O(n_1)+3O(n_3)+2O(n_4)+O(n_4.n_3)& \\ \iff T(n)=& 2O(n)+3O(n)+2O(n)+O(n^2)& \\ \iff T(n)=& 7O(n)+O(n^2)& \\ \iff T(n)=& O(n^2)& \end{array}$$

Based on the analysis conducted, the time complexity of the RBI algorithm is $O(n^2)$ or quadratic, where the step causing the high time complexity is determining the reference fluxes using FVA. This is reasonable enough because, in the FVA algorithm, the optimization process involves all metabolites, which are carried out repeatedly to predict the boundaries of all metabolic reactions.

Subsequently, simulations were conducted to assess the efficiency of the RBI algorithm in large-scale metabolic networks by measuring its running time. This simulation compared RBI-T1, RBI-T2, and RBI-T3 with PROM and TRFBA, which are the regulatory-metabolic network models that used the empirical GRNs. Additionally, five strains were employed: E. coli core, iAF1260, iJO1366, iMM904, iTO977, and Yeast7.6. Those five strain models had varying sizes of genetic regulatory networks and metabolic networks based on the number of metabolites, reactions, genes, and transcription factors provided in Table S9. In this simulation, the objective function used was the production rate of biomass.

Figure S6 showed a line graph depicting the running time of the RBI-T1, RBI-T2, RBI-T3, PROM and TRFBA algorithms on a particular model. From the graph, it is known that the RBI-T1, RBI-T2, RBI-T3, and PROM required relatively the same running time for each strain model. In addition, the increase in running time required by those algorithms is not significant. In contrast, the TRFBA algorithm requires a longer running time with a significant increase along with the increasing size of the strain model. The high running time of TRFBA might be due to the tuning process of the regulatory constraints that had a high complexity and the optimization process that used the mixed integer linear programming (MILP) model. Meanwhile, all types of RBI and PROM algorithms use FBA optimization processes that utilize a linear programming approach and do not contain a fairly complex tuning process for regulatory constraints. The average running time values obtained by RBI-T1, RBI-T2, RBI-T3, PROM, and TRFBA were 1.680, 1.869, 2.553, 1.800, and 37.258, respectively. Quantitatively, it indicated that RBI-T1 is the algorithm with the highest level of efficiency in this case, followed by PROM, RBI-T2, RBI-T3, and TRFBA.

Designing the optimal mutant strains

A comparative analysis of the proposed algorithms (RBI-T1, RBI-T2, and RBI-T3) has been performed using empirical data and validated potential TF Knockout schemes. This comparison demonstrated accurate predictions and a good correlation between the predicted outcomes and the used benchmark results. The findings indicated that the proposed algorithms were both effective and efficient in the integration of GRNs with metabolic networks for. Accordingly, in this section, the RBI-T1, RBI-T2, and RBI-T3 algorithms were utilized to engineer optimum mutant strains in E. coli and S. cerevisiae microorganisms. The design outcomes of these algorithms were compared with the PROM and TRFBA algorithms due to both algorithms’ capacity to include the empirical GRNs. The prediction results of the wild type were also provided to demonstrate the potential of the acquired mutants.

The strain models used to develop optimum mutant strains, as seen in Table S9, include E. coli and S. cerevisiae models. The E. coli model has been extensively used in metabolic engineering to predict growth rates and the production rates of targeted metabolites, such as succinate. The E. coli core and iAF1260 models have been used to assess succinate production rates using flux balance analysis (FBA) combined with a metaheuristic algorithm (Daud et al., 2019). Then, iJO1366 has been analyzed using the MoMA algorithm to forecast succinate production rates (Mienda, Shamsir & Illias, 2016). Likewise, the S. cerevisiae model has been extensively researched owing to the extensive understanding of its metabolism (Pereira, Nielsen & Rocha, 2016). Models of S. cerevisiae, including iTO977, iMM904, and Yeast 7.0, have been used to forecast significant compounds such as ethanol (Lopes & Rocha, 2017). Moreover, the yeast S. cerevisiae is the most extensively researched yeast and is used in industrial applications, including ethanol production.

Table S10 provided the predictive outcomes of the succinate production from each algorithm under both aerobic and anaerobic conditions for each strain. The substrates used for the simulation were glucose and oxygen, with the substrate uptake rate following Niu et al. (2021) in predicting the growth rate of E. coli. The proposed algorithms demonstrated excellent succinate production relative to PROM and TRFBA in almost all strains used, except in E. coli core, where its performance was inferior to them. The E. coli core model represents the most basic representation of the E. coli strain. Therefore, despite the proposed algorithms obtained a lower prediction in E. coli core, they effectively optimize the information in the advanced E. coli models, achieving a significantly higher production rate in comparison to PROM and TRFBA. Hence, the proposed algorithm generally outperformed PROM and TRFBA in succinate prediction. In addition, those results indicated the potential overproduction of the succinate production due to more than the prediction results of the wild type.

Meanwhile, in the results of designing the optimal mutant strain of S. cerevisiae for predicting ethanol production, the suggested algorithms provided competitive results compared to PROM and TRFBA, as seen in Table S11. The predictive outcomes of the RBI-T1 algorithm were marginally worse than those of PROM and TRFBA for strains iMM904 and Yeast7.6. Nonetheless, the predictive outcomes for strain iTO977 were superior. Conversely, the RBI-T2 algorithm demonstrated superior predictive outcomes compared to PROM and TRFBA for strains iTO977 and Yeast 7.6 under anaerobic circumstances, with Yeast 7.6 exhibiting the maximum ethanol output. At the same time, the RBI-T3 exhibited performance almost similar to that of the RBI-T1, which surpasses the iTO977 strain, where the forecast of ethanol production from this strain is the highest. On the other hand, based on the wild-type results, the proposed algorithm showed the potential overproduction in the particular strains, including iTO977 and Yeast 7.6, but they are under wild-type in iMM904. Nonetheless, the difference in the prediction results at iMM904 was not great, about 0.440 mmol/gDW/hr.

Subsequently, Table S12 presented the results of the optimal mutant strain schemes derived from the proposed algorithm. The findings were chosen based on the maximum metabolite production attained by the RBI algorithms, as seen in Table S10 and S11. Also, the growth rate corresponding to the production rate of the predicted metabolite was provided to identify the optimal design of the growth-coupled (GC) mutant strain capable of surviving post-mutation. The methodology used to acquire the GC mutant strain followed that of Daud et al. (2019), while the substrate uptake was based on the simulation performed by Niu et al. (2021). The table presented a scheme of mutant strains that might enhance succinate synthesis, compared to the wild-type, in the strains E. coli core (ANA), iAF1260 (AER and ANA), and iJO1366 (AER and ANA). Concurrently, excessive ethanol production was achieved in strains iTO977 (AER and ANA) and Yeast 7.6 (ANA). Here, eight of the twelve mutant strain schemes obtained have been identified and predicted to provide an overproduction of the desired metabolites, where the RBI-T2 and RBI-T3 algorithms yielded three and five optimal mutant strains, respectively.